Synthetic division is a shortcut method for dividing a polynomial by a linear factor of the form . It can be used in place of the standard long division algorithm. This method reduces the polynomial and the linear factor into a set of numeric values. After these values are processed, the resulting set of numeric outputs is used to construct the polynomial quotient and the polynomial remainder.

For an example of synthetic division, consider divided by . First, if a power of is missing from the polynomial, a term with that power and a zero coefficient must be inserted into the correct position in the polynomial. In this case the term is missing, so we must add between the cubic and linear terms:

Next, all the variables and their exponents (, , ) are removed, leaving only a list of the coefficients: 3, 0, , 2. These numbers form the dividend. We form the divisor for the synthetic division using only the constant term (2) of the linear factor . (Note: If the divisor were , we would put it in the format , resulting in a divisor of .)

The numbers representing the divisor and the dividend are placed into a division-like configuration:

The first number in the dividend (3) is put into the first position of the result area (below the horizontal line). This number is the coefficient of the 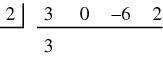term in the original polynomial:

Then this first entry in the result (3) is multiplied by the divisor (2) and the product is placed under the next term in the dividend (0):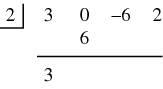

Next the number from the dividend and the result of the multiplication are added together and the sum is put in the next position on the result line: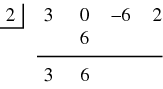

This process is continued for the remainder of the numbers in the dividend: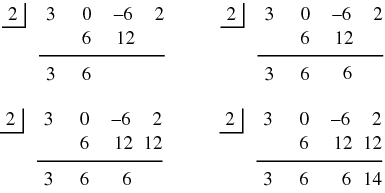

The result is the list 3, 6, 6, 14. All numbers except the last become the coefficients of the quotient polynomial. Since we started with a cubic polynomial and divided it by a linear term, the quotient is a 2nd degree polynomial:

The last entry in the result list (14) is the remainder. The quotient and remainder can be combined into one expression:

(Note that no division operations were performed to compute the answer to this division problem.)

To verify that this process has worked, we can multiply the quotient and the divisor and add the remainder to obtain the original polynomial:

			(4)
			(5)

Synthetic division can be used in conjunction with the polynomial remainder theorem to evaluate a polynomial at a real value. For example, consider the polynomial

To find the value of 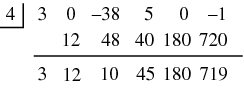, the remainder theorem states that is the remainder when is divided by . Using synthetic division, we obtain:

Therefore .