A field which is complete with respect to a discrete valuation is called a local field if its field of residue classes is finite. The Hasse principle is one of the chief applications of local field theory. A local field with field characteristic
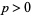
is isomorphic to the field of power series in one variable whose coefficients are in a finite field. A local field of characteristic zero is either
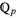
the
p-adic numbers, or power series in a complex variable.