If 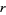 is a root of a nonzero polynomial equation
is a root of a nonzero polynomial equation
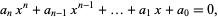 |
(1)
|
where the 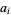 s are integers (or equivalently, rational numbers) and
s are integers (or equivalently, rational numbers) and 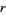 satisfies no similar equation of degree
satisfies no similar equation of degree 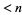 , then
, then 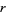 is said to be an algebraic number of degree
is said to be an algebraic number of degree 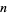 .
.
A number that is not algebraic is said to be transcendental. If 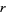 is an algebraic number and
is an algebraic number and 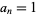 , then it is called an algebraic integer.
, then it is called an algebraic integer.
In general, algebraic numbers are complex, but they may also be real. An example of a complex algebraic number is 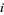 , and an example of a real algebraic number is
, and an example of a real algebraic number is 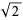 , both of which are of degree 2.
, both of which are of degree 2.
The set of algebraic numbers is denoted 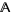 (Mathematica), or sometimes
(Mathematica), or sometimes 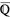 (Nesterenko 1999), and is implemented in Mathematica as Algebraics.
(Nesterenko 1999), and is implemented in Mathematica as Algebraics.
A number  can then be tested to see if it is algebraic in Mathematica using the command Element[x, Algebraics]. Algebraic numbers are represented in Mathematica as indexed polynomial roots by the symbol Root[f, n], where
can then be tested to see if it is algebraic in Mathematica using the command Element[x, Algebraics]. Algebraic numbers are represented in Mathematica as indexed polynomial roots by the symbol Root[f, n], where 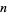 is a number from 1 to the degree of the polynomial (represented as a so-called "pure function")
is a number from 1 to the degree of the polynomial (represented as a so-called "pure function") 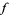 .
.
Examples of some significant algebraic numbers and their degrees are summarized in the following table.
| constant |
degree |
Conway's constant 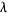 |
71 |
Delian constant 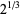 |
3 |
disk covering problem 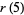 |
8 |
| Freiman's constant |
2 |
golden ratio 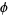 |
2 |
golden ratio conjugate 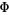 |
2 |
Graham's biggest little hexagon area 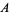 |
10 |
hard hexagon entropy constant 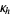 |
24 |
| heptanacci constant |
7 |
| hexanacci constant |
6 |
| i |
2 |
| Lieb's square ice constant |
2 |
logistic map 3-cycle onset 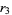 |
2 |
logistic map 4-cycle onset 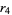 |
2 |
logistic map 5-cycle onset 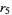 |
22 |
logistic map 6-cycle onset 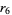 |
40 |
logistic map 7-cycle onset 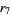 |
114 |
logistic map 8-cycle onset 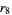 |
12 |
logistic map 16-cycle onset 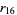 |
240 |
| pentanacci constant |
5 |
| plastic constant |
3 |
Pythagoras's constant 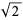 |
2 |
| silver constant |
3 |
| silver ratio |
2 |
| tetranacci constant |
4 |
| Theodorus's constant |
2 |
| tribonacci constant |
3 |
| twenty-vertex entropy constant |
2 |
| Wallis's constant |
3 |
If, instead of being integers, the 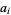 s in the above equation are algebraic numbers
s in the above equation are algebraic numbers 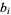 , then any root of
, then any root of
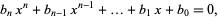 |
(2)
|
is an algebraic number.
If 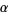 is an algebraic number of degree
is an algebraic number of degree 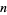 satisfying the polynomial equation
satisfying the polynomial equation
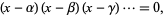 |
(3)
|
then there are 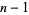 other algebraic numbers
other algebraic numbers 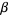 ,
, 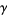 , ... called the conjugates of
, ... called the conjugates of 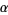 . Furthermore, if
. Furthermore, if 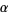 satisfies any other algebraic equation, then its conjugates also satisfy the same equation (Conway and Guy 1996).
satisfies any other algebraic equation, then its conjugates also satisfy the same equation (Conway and Guy 1996).