It is possible to perform multiplication of large numbers in (many) fewer operations than the usual brute-force technique of "long multiplication." As discovered by Karatsuba (Karatsuba and Ofman 1962), multiplication of two 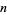 -digit numbers can be done with a bit complexity of less than
-digit numbers can be done with a bit complexity of less than 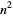 using identities of the form
using identities of the form
![(a+b·10^n)(c+d·10^n)=ac+[(a+b)(c+d)-ac-bd]10^n+bd·10^(2n).](http://mathworld.wolfram.com/images/equations/KaratsubaMultiplication/NumberedEquation1.gif) |
(1)
|
Proceeding recursively then gives bit complexity 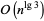 , where
, where 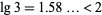 (Borwein et al. 1989). The best known bound is
(Borwein et al. 1989). The best known bound is 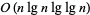 steps for
steps for 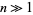 (Schönhage and Strassen 1971, Knuth 1998). However, this algorithm is difficult to implement, but a procedure based on the fast Fourier transform is straightforward to implement and gives bit complexity
(Schönhage and Strassen 1971, Knuth 1998). However, this algorithm is difficult to implement, but a procedure based on the fast Fourier transform is straightforward to implement and gives bit complexity 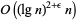 (Brigham 1974, Borodin and Munro 1975, Borwein et al. 1989, Knuth 1998).
(Brigham 1974, Borodin and Munro 1975, Borwein et al. 1989, Knuth 1998).
As a concrete example, consider multiplication of two numbers each just two "digits" long in base 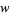 ,
,
then their product is
Instead of evaluating products of individual digits, now write
The key term is 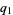 , which can be expanded, regrouped, and written in terms of the
, which can be expanded, regrouped, and written in terms of the 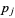 as
as
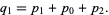 |
(10)
|
However, since 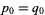 , and
, and 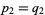 , it immediately follows that
, it immediately follows that
so the three "digits" of 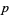 have been evaluated using three multiplications rather than four. The technique can be generalized to multidigit numbers, with the trade-off being that more additions and subtractions are required.
have been evaluated using three multiplications rather than four. The technique can be generalized to multidigit numbers, with the trade-off being that more additions and subtractions are required.
Now consider four-"digit" numbers
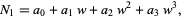 |
(14)
|
which can be written as a two-"digit" number represented in the base 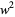 ,
,
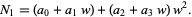 |
(15)
|
The "digits" in the new base are now
and the Karatsuba algorithm can be applied to 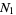 and
and 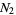 in this form. Therefore, the Karatsuba algorithm is not restricted to multiplying two-digit numbers, but more generally expresses the multiplication of two numbers in terms of multiplications of numbers of half the size. The asymptotic speed the algorithm obtains by recursive application to the smaller required subproducts is
in this form. Therefore, the Karatsuba algorithm is not restricted to multiplying two-digit numbers, but more generally expresses the multiplication of two numbers in terms of multiplications of numbers of half the size. The asymptotic speed the algorithm obtains by recursive application to the smaller required subproducts is 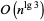 (Knuth 1998).
(Knuth 1998).
When this technique is recursively applied to multidigit numbers, a point is reached in the recursion when the overhead of additions and subtractions makes it more efficient to use the usual 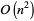 multiplication algorithm to evaluate the partial products. The most efficient overall method therefore relies on a combination of Karatsuba and conventional multiplication.
multiplication algorithm to evaluate the partial products. The most efficient overall method therefore relies on a combination of Karatsuba and conventional multiplication.