Archimedes' axiom, also known as the continuity axiom or Archimedes' lemma, survives in the writings of Eudoxus (Boyer and Merzbach 1991), but the term was first coined by the Austrian mathematician Otto Stolz (1883). It states that, given two magnitudes having a ratio, one can find a multiple of either which will exceed the other. This principle was the basis for the method of exhaustion, which Archimedes invented to solve problems of area and volume.
Symbolically, the axiom states that
iff the appropriate one of following conditions is satisfied for integers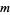 
and 
:
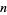1. If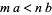 
, then 
.
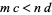2. If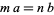 
, then 
.
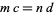3. If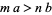 
, then 
.
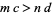Formally, Archimedes' axiom states that if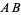 
and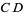 
are two line segments, then there exist a finite number of points 
, 
, ..., 
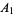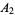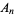on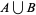 
such that
and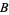 
is between 
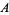and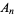 
(Itô 1986, p. 611). A geometry in which Archimedes' lemma does not hold is called a non-Archimedean Geometry.
