A Pisot number is a positive algebraic integer greater than 1 all of whose conjugate elements have absolute value less than 1. A real quadratic algebraic integer greater than 1 and of degree 2 or 3 is a Pisot number if its norm is equal to 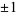 . The golden ratio
. The golden ratio  (denoted
(denoted  when considered as a Pisot number) is an example of a Pisot number since it has degree two and norm
when considered as a Pisot number) is an example of a Pisot number since it has degree two and norm 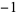 .
.
The smallest Pisot number is given by the positive root 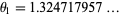 (Sloane's A060006) of
(Sloane's A060006) of
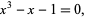 |
(1)
|
known as the plastic constant. This number was identified as the smallest known by Salem (1944), and proved to be the smallest possible by Siegel (1944).
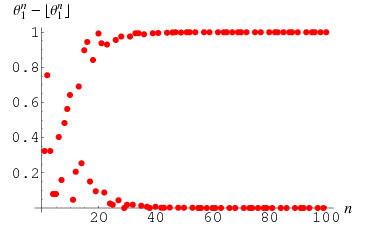
Pisot constants give rise to almost integers. For example, the larger the power to which 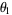 is taken, the closer
is taken, the closer 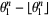 , where
, where 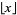 is the floor function, is to either 0 or 1 (Trott 2004). For example, the spectacular example
is the floor function, is to either 0 or 1 (Trott 2004). For example, the spectacular example 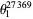 is within
is within 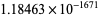 of an integer (Trott 2004, pp. 8-9).
of an integer (Trott 2004, pp. 8-9).
The powers of 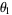 for which this quantity is closer to 0 are 1, 3, 4, 5, 6, 7, 8, 11, 12, 14, 17, ... (Sloane's A051016), while those for which it is closer to 1 are 2, 9, 10, 13, 15, 16, 18, 20, 21, 23, ... (Sloane's A051017).
for which this quantity is closer to 0 are 1, 3, 4, 5, 6, 7, 8, 11, 12, 14, 17, ... (Sloane's A051016), while those for which it is closer to 1 are 2, 9, 10, 13, 15, 16, 18, 20, 21, 23, ... (Sloane's A051017).
Siegel also identified the second smallest Pisot numbers as the positive root 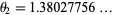 (Sloane's A086106) of
(Sloane's A086106) of
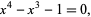 |
(2)
|
showed that 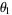 and
and 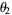 are isolated, and showed that the positive roots of each polynomial
are isolated, and showed that the positive roots of each polynomial
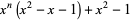 |
(3)
|
for 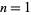 , 2, 3, ...,
, 2, 3, ...,
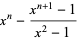 |
(4)
|
for 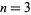 , 5, 7, ..., and
, 5, 7, ..., and
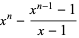 |
(5)
|
for 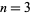 , 5, 7, ... are Pisot numbers.
, 5, 7, ... are Pisot numbers.
All the Pisot numbers less than 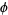 are known (Dufresnoy and Pisot 1955). Some small Pisot numbers and their polynomials are given in the following table. The latter two entries are from Boyd (1977).
are known (Dufresnoy and Pisot 1955). Some small Pisot numbers and their polynomials are given in the following table. The latter two entries are from Boyd (1977).
| number |
Sloane |
order |
polynomial coefficients |
| 1.3247179572 |
A060006 |
3 |
1 0 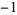 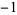 |
| 1.3802775691 |
A086106 |
4 |
1 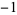 0 0 0 0 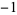 |
| 1.6216584885 |
|
16 |
1 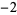 2 2 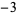 2 2 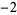 1 0 0 1 1 0 0 1 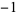 2 2 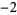 2 2 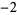 1 1 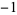 |
| 1.8374664495 |
|
20 |
1 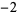 0 1 0 1 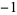 0 1 0 1 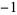 0 1 0 0 1 0 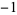 0 1 0 1 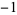 0 1 0 1 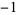 0 1 0 1 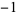 |
Pisot numbers originally arose in the consideration of
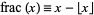 |
(6)
|
where 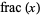 denotes the fractional part of
denotes the fractional part of  and
and 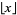 is the floor function. Letting
is the floor function. Letting 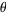 be a number greater than 1 and
be a number greater than 1 and 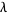 a positive number, for a given
a positive number, for a given 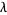 , the sequence of numbers
, the sequence of numbers 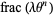 for
for 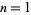 , 2, ... is an equidistributed sequence in the interval (0, 1) when
, 2, ... is an equidistributed sequence in the interval (0, 1) when 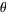 does not belong to a
does not belong to a 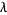 -dependent exceptional set
-dependent exceptional set 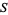 of measure zero (Koksma 1935). Pisot (1938) and Vijayaraghavan (1941) independently studied the exceptional values of
of measure zero (Koksma 1935). Pisot (1938) and Vijayaraghavan (1941) independently studied the exceptional values of 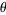 , and Salem (1943) proposed calling such values Pisot-Vijayaraghavan numbers.
, and Salem (1943) proposed calling such values Pisot-Vijayaraghavan numbers.
Pisot (1938) subsequently proved the fact that if 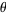 is chosen such that there exists a
is chosen such that there exists a 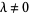 for which the series
for which the series
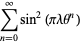 |
(7)
|
converges, then 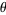 is an algebraic integer whose conjugates all (except for itself) have modulus
is an algebraic integer whose conjugates all (except for itself) have modulus 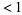 , and
, and 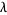 is an algebraic integer of the field
is an algebraic integer of the field 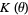 . Vijayaraghavan (1940) proved that the set of Pisot numbers has infinitely many limit points. Salem (1944) proved that the set of Pisot numbers is closed. The proof of this theorem is based on the lemma that for a Pisot number
. Vijayaraghavan (1940) proved that the set of Pisot numbers has infinitely many limit points. Salem (1944) proved that the set of Pisot numbers is closed. The proof of this theorem is based on the lemma that for a Pisot number 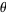 , there always exists a number
, there always exists a number 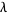 such that
such that 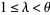 and the following inequality is satisfied:
and the following inequality is satisfied:
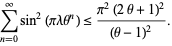 |
(8)
|