A global field is either a number field, a function field on an algebraic curve, or an extension of transcendence degree one over a finite field. From a modern point of view, a global field may refer to a function field on a complex algebraic curve as well as one over a finite field. A global field contains a canonical subring, either the algebraic integers or the polynomials. By choosing a prime ideal in its subring, a global field can be topologically completed to give a local field. For example, the rational numbers are a global field. By choosing a prime number 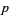, the rationals can be completed in the p-adic norm to form the p-adic numbers .

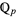A global field is called global because of the special case of a complex algebraic curve, for which the field consists of global functions (i.e., functions that are defined everywhere). These functions differ from functions defined near a point, whose completion is called a local field. Under favorable conditions, the local information can be patched together to yield global information (e.g., the Hasse principle).