An infinite sequence of positive integers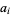 
satisfying
 |
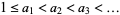(1)
|
is an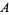 
-sequence if no 
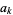is the sum of two or more distinct earlier terms (Guy 1994). Such sequences are sometimes also known as sum-free sets.
Erdős (1962) proved
 |
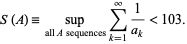(2)
|
Any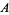 
-sequence satisfies the chi inequality (Levine and O'Sullivan 1977), which gives 
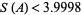. Abbott (1987) and Zhang (1992) have given a bound from below, so the best result to date is
 |
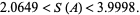(3)
|
Levine and O'Sullivan (1977) conjectured that the sum of reciprocals of an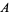 
-sequence satisfies
 |
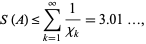(4)
|
where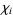 
are given by the Levine-O'Sullivan greedy algorithm. However, summing the first 
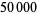terms of the Levine-O'Sullivan sequence already gives 3.0254....
