The simplification of a fraction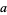 
which gives a correct answer by "canceling" digits of 
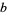and 
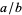. There are only four such cases for numerator and denominators of two digits in base 10: 
, 
, 
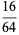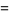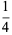, and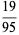 
(Boas 1979). The set of all proper solutions up to 3-digit denominators is given by 13/325, 16/64, 19/95, 26/65, 124/217, 127/762, 138/184, 139/973, 145/435, 148/185, 154/253, 161/644, 163/326, 166/664, 176/275, 182/819, 187/286, 187/385, 187/748, 199/995, 218/981, 266/665, 273/728, 275/374, 286/385, 316/632, 327/872, 364/637, 412/721, and 436/763.
The concept of anomalous cancellation can be extended to arbitrary bases. prime bases have no solutions, but there is a solution corresponding to each proper divisor of a composite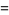 
. When 
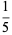is prime, this type of solution is the only one. For base 4, for example, the only solution is 
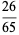. Boas gives a table of solutions for 
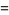. The number of solutions is even unless 
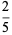is an even square.
 |
 |
 |
 |
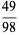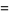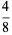| 4 |
1 |
26 |
4 |
| 6 |
2 |
27 |
6 |
| 8 |
2 |
28 |
10 |
| 9 |
2 |
30 |
6 |
| 10 |
4 |
32 |
4 |
| 12 |
4 |
34 |
6 |
| 14 |
2 |
35 |
6 |
| 15 |
6 |
36 |
21 |
| 16 |
7 |
38 |
2 |
| 18 |
4 |
39 |
6 |
| 20 |
4 |
|
|
| 21 |
10 |
|
|
| 22 |
6 |
|
|
| 24 |
6 |
|
|
