The negabinary representation of a number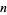 
is its representation in base 
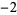(i.e., base negative 2). It is therefore given by the coefficients 
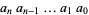in
where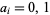 
.
Conversion of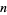 
to negabinary can be done using the Mathematica code
Negabinary[n_Integer] := Module[
{t = (2/3)(4^Floor[Log[4, Abs[n] + 1] + 2] - 1)},
IntegerDigits[BitXor[n + t, t], 2]
]
due to D. Librik (Szudzik). The bitwise XOR portion is originally due to Schroeppel (1972), who noted that the sequence of bits in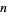 
is given by 
.
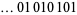The following table gives the negabinary representations for the first few integers (Sloane's A039724).
 |
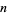negabinary |
 |
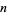negabinary |
| 1 |
1 |
11 |
11111 |
| 2 |
110 |
12 |
11100 |
| 3 |
111 |
13 |
11101 |
| 4 |
100 |
14 |
10010 |
| 5 |
101 |
15 |
10011 |
| 6 |
11010 |
16 |
10000 |
| 7 |
11011 |
17 |
10001 |
| 8 |
11000 |
18 |
10110 |
| 9 |
11001 |
19 |
10111 |
| 10 |
11110 |
20 |
10100 |
If these numbers are interpreted as binary numbers and converted to decimal, their values are 1, 6, 7, 4, 5, 26, 27, 24, 25, 30, 31, 28, 29, 18, 19, 16, ... (Sloane's A005351). The numbers having the same representation in binary and negabinary are members of the Moser-de Bruijn sequence, 0, 1, 4, 5, 16, 17, 20, 21, 64, 65, 68, 69, 80, 81, ... (Sloane's A000695).
