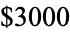
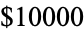
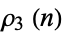
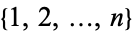
Erdős offered a prize for a proof of the proposition that "If the sum of reciprocals of a set of integers diverges, then that set contains arbitrarily long arithmetic progressions." This conjecture is still open (unsolved), even for 3-term arithmetic progressions. Erdős also offered for an asymptotic formula for , the largest possible cardinality of a subset of that does not contain a 3-term arithmetic progression.