Pick any two coprime integers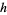 
and 
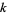, then the circle 
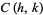of radius 
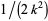centered at 
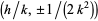is known as a Ford circle. No matter what and how many 
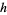s and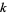 
s are picked, none of the Ford circles intersect (and all are tangent to the x-axis). This can be seen by examining the squared distance between the centers of the circles with 
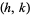and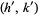 
,
 |
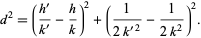(1)
|
Let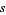 
be the sum of the radii
 |
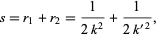(2)
|
then
 |
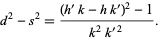(3)
|
But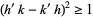 
, so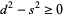 
and the distance between circle centers is 
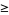the sum of the circle radii, with equality (and therefore tangency) iff 
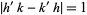. Ford circles are related to the Farey sequence (Conway and Guy 1996).
If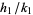 
, 
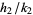, and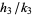 
are three consecutive terms in a Farey sequence, then the circles 
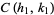and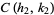 
are tangent at
 |
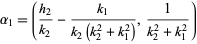(4)
|
and the circles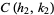 
and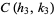 
intersect in
 |
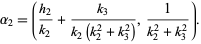(5)
|
Moreover,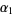 
lies on the circumference of the semicircle with diameter 
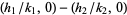and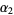 
lies on the circumference of the semicircle with diameter 
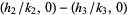(Apostol 1997, p. 101).
