The function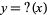 
defined by Minkowski for the purpose of mapping the quadratic irrational numbers in the open interval 
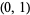into the rational numbers of 
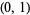in a continuous, order-preserving manner. 
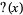takes a number having continued fraction ![x=[0;a_1,a_2,a_3,...]](http://mathworld.wolfram.com/images/equations/MinkowskisQuestionMarkFunction/Inline5.gif)
to the number
 |
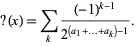(1)
|
The function satisfies the following properties (Salem 1943).
1. 
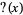is strictly increasing.
2. If 
is rational, then 
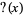is of the form 
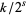, with 
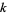and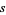 
integers.
3. If 
is a quadratic irrational number, then the continued fraction is periodic, and hence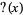 
is rational.
4. The function is purely singular (Denjoy 1938).
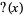can also be constructed as
 |
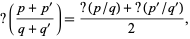(2)
|
where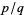 
and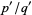 
are two consecutive irreducible fractions from the Farey sequence. At the 
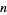th stage of this definition, 
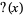is defined for 
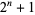values of 
, and the ordinates corresponding to these values are 
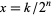for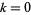 
, 1, ..., 
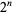(Salem 1943).
The function satisfies the identity
 |
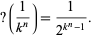(3)
|
A few special values include
where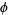 
is the golden ratio.
