A number 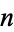is called an Egyptian number if it is the sum of the denominators in some unit fraction representation of a positive whole number not consisting entirely of 1s. For example,

so 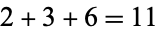is an Egyptian number. The numbers that are not Egyptian are 2, 3, 5, 6, 7, 8, 12, 13, 14, 15, 19, 21, and 23 (Sloane's A028229; Konhauser et al. 1996, p. 147).

If 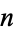is the sum of denominators of a unit fraction representation composed of distinct denominators which are not all 1s, then it is called a strictly Egyptian number. For example, by virtue of

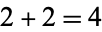is Egyptian, but it is not strictly Egyptian. Graham (1963) proved that every number 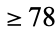is strictly Egyptian. Numbers that are strictly Egyptian are 11, 24, 30, 31, 32, 37, 38, 43, ... (Sloane's A052428), and those which are not are 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, ... (Sloane's A051882).