An infinite sequence of positive integers
 |
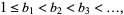(1)
|
also called a Sidon sequence, such that all pairwise sums
 |
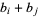(2)
|
for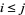 
are distinct (Guy 1994). An example is 1, 2, 4, 8, 13, 21, 31, 45, 66, 81, 97, 123, 148, 182, 204, 252, 290, 361, ... (Sloane's A005282). Halberstam and Roth (1983) contains an accessible account of most known results up to around 1965. Recent advances have been made by Cilleruelo, Jia, Kolountzakis, Lindstrom, and Ruzsa.
Zhang (1993, 1994) showed that
 |
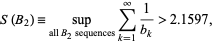(3)
|
which has been increased to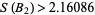 
by R. Lewis using the non-
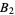sequence 1, 2, 4, 8, 13, 21, 31, 45, 66, 81, 97, 123, 148, 182, 204, 252, 291, 324, ... (Sloane's A046185). The definition can be extended to 
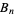-sequences (Guy 1994).
