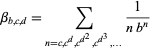A number is said to be simply normal to base 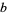 if its base-
if its base-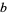 expansion has each digit appearing with average frequency tending to
expansion has each digit appearing with average frequency tending to 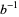 .
.
A normal number is an irrational number for which any finite pattern of numbers occurs with the expected limiting frequency in the expansion in a given base (or all bases). For example, for a normal decimal number, each digit 0-9 would be expected to occur 1/10 of the time, each pair of digits 00-99 would be expected to occur 1/100 of the time, etc. A number that is normal in base-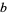 is often called
is often called 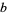 -normal.
-normal.
A number that is 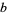 -normal for every
-normal for every 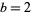 , 3, ... is said to be absolutely normal (Bailey and Crandall 2003).
, 3, ... is said to be absolutely normal (Bailey and Crandall 2003).
As stated by Kac (1959), "As is often the case, it is much easier to prove that an overwhelming majority of objects possess a certain property than to exhibit even one such object....It is quite difficult to exhibit a 'normal' number!" (Stoneham 1970).
If a real number 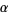 is
is 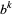 -normal, then it is also
-normal, then it is also 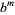 -normal for
-normal for 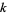 and
and 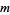 integers (Kuipers and Niederreiter 1974, p. 72; Bailey and Crandall 2001). Furthermore, if
integers (Kuipers and Niederreiter 1974, p. 72; Bailey and Crandall 2001). Furthermore, if 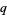 and
and 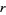 are rational with
are rational with 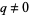 and
and 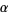 is
is 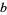 -normal, then so is
-normal, then so is 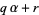 , while if
, while if 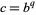 is an integer, then
is an integer, then 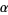 is also
is also 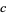 -normal (Kuipers and Niederreiter 1974, p. 77; Bailey and Crandall 2001).
-normal (Kuipers and Niederreiter 1974, p. 77; Bailey and Crandall 2001).
Determining if numbers are normal is an unresolved problem. It is not even known if fundamental mathematical constants such as pi (Wagon 1985, Bailey and Crandall 2003), the natural logarithm of 2 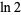 (Bailey and Crandall 2003), Apéry's constant
(Bailey and Crandall 2003), Apéry's constant 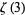 (Bailey and Crandall 2003), Pythagoras's constant
(Bailey and Crandall 2003), Pythagoras's constant 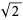 (Bailey and Crandall 2003), and e are normal, although the first 30 million digits of
(Bailey and Crandall 2003), and e are normal, although the first 30 million digits of 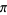 are very uniformly distributed (Bailey 1988).
are very uniformly distributed (Bailey 1988).
While tests of 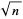 for
for 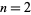 , 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15 indicate that these square roots may be normal (Beyer et al. 1970ab), normality of these numbers has (possibly until recently) also not been proven. Isaac (2005) recently published a preprint that purports to show that each number of the form
, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15 indicate that these square roots may be normal (Beyer et al. 1970ab), normality of these numbers has (possibly until recently) also not been proven. Isaac (2005) recently published a preprint that purports to show that each number of the form 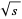 for
for 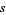 not a perfect square is simply normal to the base 2. Unfortunately, this work uses a nonstandard approach that appears rather cloudy to at least some experts who have looked at it.
not a perfect square is simply normal to the base 2. Unfortunately, this work uses a nonstandard approach that appears rather cloudy to at least some experts who have looked at it.
While Borel (1909) proved the normality of almost all numbers with respect to Lebesgue measure, with the exception of a number of special classes of constants (e.g., Stoneham 1973, Korobov 1990, Bailey and Crandall 2003), the only numbers known to be normal (in certain bases) are artificially constructed ones such as the Champernowne constant and the Copeland-Erdős constant. In particular, the binary Champernowne constant
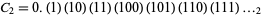 |
(1)
|
(Sloane's A030190) is 2-normal (Bailey and Crandall 2001).
Bailey and Crandall (2001) showed that, subject to an unproven but reasonable hypothesis related to pseudorandom number generators, the constants 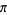 ,
, 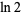 , and
, and 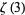 would be 2-normal, where
would be 2-normal, where 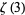 is Apéry's constant. Stoneham (1973) proved that the so-called Stoneham numbers
is Apéry's constant. Stoneham (1973) proved that the so-called Stoneham numbers
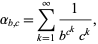 |
(2)
|
where 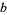 and
and 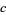 are relatively prime positive integers, are
are relatively prime positive integers, are 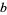 -normal whenever
-normal whenever 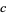 is an odd prime
is an odd prime 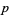 and
and 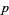 is a primitive root of
is a primitive root of 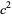 . This result was extended by Bailey and Crandall (2003), who showed that
. This result was extended by Bailey and Crandall (2003), who showed that 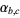 is normal for all positive integers
is normal for all positive integers 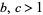 provided only that
provided only that 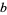 and
and 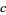 are relatively prime.
are relatively prime.
Korobov (1990) showed that the constants
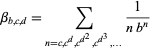 |
(3)
|
are 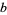 -normal for
-normal for 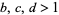 positive integers and
positive integers and 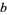 and
and 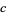 relatively prime, a result reproved using completely different techniques by Bailey and Crandall (2003). Amazingly, Korobov (1990) also gave an explicit algorithm for computing terms in the continued fraction of
relatively prime, a result reproved using completely different techniques by Bailey and Crandall (2003). Amazingly, Korobov (1990) also gave an explicit algorithm for computing terms in the continued fraction of 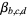 .
.
Bailey and Crandall (2003) also established 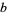 -normality for constants of the form
-normality for constants of the form 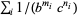 for certain sequences of integers
for certain sequences of integers 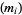 and
and 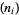 .
.