The negadecimal representation of a number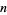 
is its representation in base 
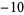(i.e., base negative 10). It is therefore given by the coefficients 
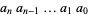in
where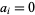 
, 1, ..., 9.
The negadecimal digits may be obtained with the Mathematica code
Negadecimal[0] := {0}
Negadecimal[i_] := Rest @ Reverse @
Mod[NestWhileList[(# - Mod[#, 10])/-10&,
i, # != 0& ], 10]
The following table gives the negadecimal representations for the first few integers (A039723).
 |
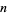negadecimal |
 |
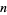negadecimal |
 |
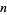negadecimal |
| 1 |
1 |
11 |
191 |
21 |
181 |
| 2 |
2 |
12 |
192 |
22 |
182 |
| 3 |
3 |
13 |
193 |
23 |
183 |
| 4 |
4 |
14 |
194 |
24 |
184 |
| 5 |
5 |
15 |
195 |
25 |
185 |
| 6 |
6 |
16 |
196 |
26 |
186 |
| 7 |
7 |
17 |
197 |
27 |
187 |
| 8 |
8 |
18 |
198 |
28 |
188 |
| 9 |
9 |
19 |
199 |
29 |
189 |
| 10 |
190 |
20 |
180 |
30 |
170 |
The numbers having the same decimal and negadecimal representations are those which are sums of distinct powers of 100: 1, 2, 3, 4, 5, 6, 7, 8, 9, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 200, ... (Sloane's A051022).
