|
|
Pandigital Fraction
A fraction containing each of the digits 1 through 9 is called a pandigital fraction. The following table gives the number of pandigital fractions which represent simple unit fractions. The numbers of pandigital fractions for 1/1, 1/2, 1/3, ... are 0, 12, 2, 4, 12, 3, 7, 46, 3, ... (Sloane's A054383).
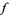 |
# |
fractions |
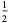 |
12 |
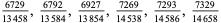 , , |
| |
|
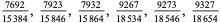 |
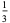 |
2 |
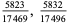 |
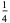 |
4 |
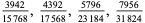 |
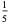 |
12 |
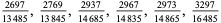 , , |
| |
|
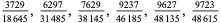 |
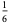 |
3 |
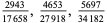 |
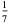 |
7 |
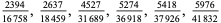 , , |
| |
|
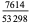 |
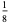 |
46 |
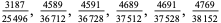 , , |
| |
|
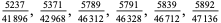 , , |
| |
|
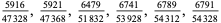 , , |
| |
|
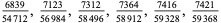 , , |
| |
|
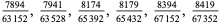 , , |
| |
|
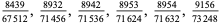 , , |
| |
|
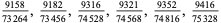 , , |
| |
|
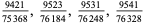 |
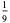 |
3 |
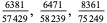 |
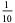 |
0 |
|
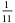 |
0 |
|
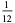 |
4 |
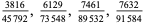 |
Bugün 51 ziyaretçi (62 klik) kişi burdaydı!
|
|