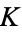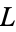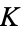The Chebotarev density theorem is a complicated theorem in algebraic number theory which yields an asymptotic formula for the density of prime ideals of a number field that split in a certain way in an algebraic extension of . When the base field is the field 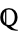of rational numbers, the theorem becomes much simpler.

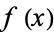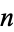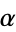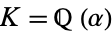Let be a monic irreducible polynomial of degree with integer coefficients with root , let , let 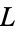be the normal closure of 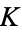, and let 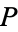be a partition 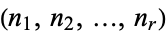of 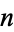, i.e., an ordered set of positive integers 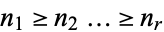with 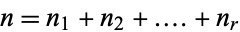. A prime is said to be unramified (over the number field 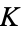) if it does not divide the discriminant of 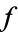. Let 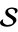denote the set of unramified primes. Consider the set 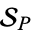of unramified primes for which 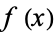factors as 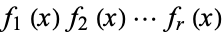modulo 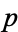, where 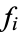is irreducible modulo 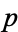and has degree 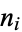. Also define the density 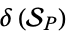of primes in 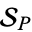as follows:

Now consider the Galois group 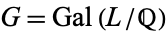of the number field 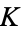. Since this is a subgroup of the symmetric group 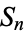, every element of 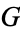can be represented as a permutation of 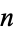letters, which in turn has a unique representation as a product of disjoint cycles. Now consider the set of elements 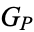of 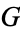consisting of disjoint cycles of length 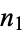, , 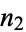..., 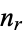. Then .

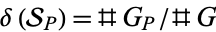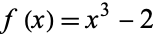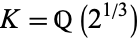As an example, let , so and 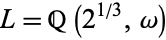, where 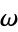is a primitive root of unity. Since 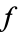has discriminant 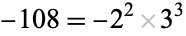, the only ramified primes are 2 and 3.

Let 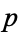be an unramified prime. Then 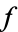has a root (mod 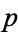) if and only if 2 has a cube root (mod 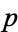), which occurs whenever 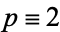(mod 3) or 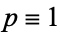(mod 3) and 2 has multiplicative order modulo 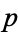dividing 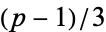. The first case occurs for half of all unramified primes and the second case occurs for one sixth of all primes. In the first case, 2 has a unique cube root modul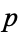o , so 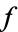factors as the product of a linear and an irreducible quadratic factor mod 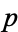. In the second case, 2 has three distinct cube roots mod 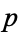, so 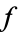has three linear factors mod 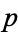. In the remaining case, which occurs for 1/3 of all unramified primes, 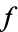is irreducible mod 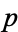. Now consider the corresponding elements of 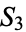. The first case corresponds to products of 2-cycles and 1-cycles (the identity), of which there are three, or half of the elements of 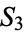, the second case corresponds to products of three 1-cycles, or the identity, of which there is just one element, or one sixth of the elements of 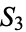, and the remaining case corresponds to 3-cycles, of which there are two, or one third the elements of 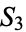. Since 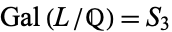in this case, the Chebotarev density theorem holds for this example.

The Chebotarev density theorem can often be used to determine the Galois group of a given irreducible polynomial 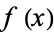of degree 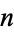. To do so, count the number of unramified primes up to a specified bound for which 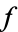factors in a certain way and then compare the results with the fractions of elements of each of the transitive subgroups of 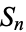with the same cyclic structure. Lenstra provides some good examples of this procedure.