A cyclotomic field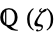 
is obtained by adjoining a primitive root of unity 
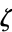, say 
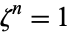, to the rational numbers 
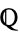. Since 
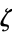is primitive, 
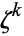is also an 
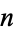th root of unity and 
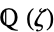contains all of the 
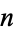th roots of unity,
 |
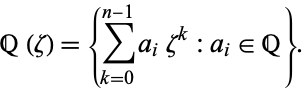(1)
|
For example, when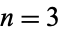 
and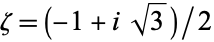 
, the cyclotomic field is a quadratic field
where the coefficients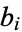 
are contained in 
.
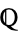The Galois group of a cyclotomic field over the rationals is the multiplicative group of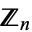 
, the ring of integers (mod 
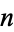). Hence, a cyclotomic field is a Abelian extension. Not all cyclotomic fields have unique factorization, for instance, 
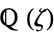, where 
.
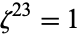