|
|
Algebraic Curves-Mordell Curve
An elliptic curve of the form 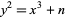 for for 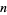 an integer. This equation has a finite number of solutions in integers for all nonzero an integer. This equation has a finite number of solutions in integers for all nonzero 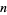 . If . If 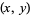 is a solution, it therefore follows that is a solution, it therefore follows that 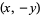 is as well. is as well.
Uspensky and Heaslet (1939) give elementary solutions for 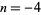 , , 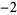 , and 2, and then give , and 2, and then give 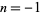 , , 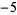 , , 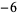 , and 1 as exercises. Euler found that the only integer solutions to the particular case , and 1 as exercises. Euler found that the only integer solutions to the particular case 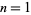 (a special case of Catalan's conjecture) are (a special case of Catalan's conjecture) are 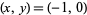 , , 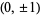 , and , and 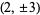 . This can be proved using Skolem's method, using the Thue equation . This can be proved using Skolem's method, using the Thue equation 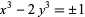 , using 2-descent to show that the elliptic curve has rank 0, and so on. It is given as exercise 6b in Uspensky and Heaslet (1939, p. 413), and proofs published by Wakulicz (1957), Mordell (1969, p. 126), Sierpiński and Schinzel (1988, pp. 75-80), and Metsaenkylae (2003). , using 2-descent to show that the elliptic curve has rank 0, and so on. It is given as exercise 6b in Uspensky and Heaslet (1939, p. 413), and proofs published by Wakulicz (1957), Mordell (1969, p. 126), Sierpiński and Schinzel (1988, pp. 75-80), and Metsaenkylae (2003).
Solutions of the Mordell curve with 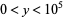 are summarized in the table below for small are summarized in the table below for small 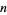 . .
 |
solutions |
| 1 |
(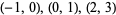 , 0), (0, 1), (2, 3) , 0), (0, 1), (2, 3) |
| 2 |
(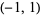 , 1) , 1) |
| 3 |
(1, 2) |
| 4 |
(0, 2) |
| 5 |
(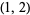 , 2) , 2) |
| 6 |
none |
| 7 |
none |
| 8 |
(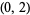 , 0), (1, 3), (2, 4), (46, 312) , 0), (1, 3), (2, 4), (46, 312) |
| 9 |
(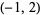 , 1), (0, 3), (3, 6), (6, 15), (40, 253) , 1), (0, 3), (3, 6), (6, 15), (40, 253) |
| 10 |
(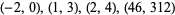 , 3) , 3) |
Values of 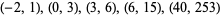 such that the Mordell curve has no integer solutions are given by 6, 7, 11, 13, 14, 20, 21, 23, 29, 32, 34, 39, 42, ... (Sloane's A054504; Apostol 1976, p. 192). such that the Mordell curve has no integer solutions are given by 6, 7, 11, 13, 14, 20, 21, 23, 29, 32, 34, 39, 42, ... (Sloane's A054504; Apostol 1976, p. 192).
Bugün 12 ziyaretçi (19 klik) kişi burdaydı!
|
|