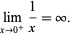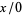Division by zero is the operation of taking the quotient of any number and 0, i.e., . The uniqueness of division breaks down when dividing by zero, since the product 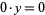is the same for any 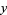, so 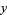cannot be recovered by inverting the process of multiplication. 0 is the only number with this property and, as a result, division by zero is undefined for real numbers and can produce a fatal condition called a "division by zero error" in computer programs.

To the persistent but misguided reader who insists on asking "What happens if I do divide by zero," Derbyshire (2004, p. 36) provides the slightly flippant but firm and concise response, "You can't. It's against the rules." Even in fields other than the real numbers, division by zero is never allowed (Derbyshire 2004, p. 266).

There are, however, contexts in which division by zero can be considered as defined. For example, division by zero 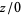for 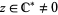in the extended complex plane C-* is defined to be a quantity known as complex infinity. This definition expresses the fact that, for 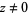, 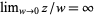(i.e., complex infinity). However, even though the formal statement 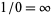is permitted in C-*, note that this does not mean that 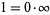. Zero does not have a multiplicative inverse under any circumstances.

Although division by zero is not defined for reals, limits involving division by a real quantity which approaches zero may in fact be well-defined. For example,

Of course, such limits may also approach infinity,