The three-dimensional analog of the Sierpiński sieve illustrated above, also called the Sierpiński sponge or Sierpiński tetrahedron. Let 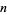be the number of tetrahedra, 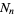the length of a side, and 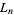the fractional volume of tetrahedra after the 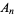th iteration. Then

			(1)
			(2)
			(3)

The capacity dimension is therefore

			(4)
			(5)

so the tetrix has an integer capacity dimension (which is one less than the dimension of the three-dimensional tetrahedra from which it is built), despite the fact that it is a fractal.

The following illustrations demonstrate how the dimension of the tetrix can be the same as that of the plane by showing three stages of the rotation of a tetrix, viewed along one of its edges. In the last frame, the tetrix "looks" like the two-dimensional plane.