Koch Snowflake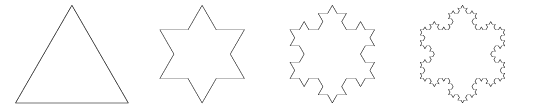 A fractal, also known as the Koch island, which was first described by Helge von Koch in 1904. It is built by starting with an equilateral triangle, removing the inner third of each side, building another equilateral triangle at the location where the side was removed, and then repeating the process indefinitely. The Koch snowflake can be simply encoded as a Lindenmayer system with initial string "F--F--F", string rewriting rule "F" -> "F+F--F+F", and angle 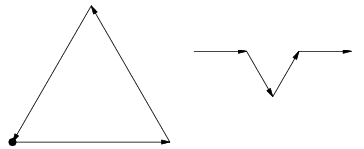 Let
Solving the recurrence equation with
so as
The capacity dimension is then
(Sloane's A100831).  Some beautiful tilings, a few examples of which are illustrated above, can be made with iterations toward Koch snowflakes.  In addition, two sizes of Koch snowflakes in area ratio 1:3 tile the plane, as shown above.  Another beautiful modification of the Koch snowflake involves inscribing the constituent triangles with filled-in triangles, possibly rotated at some angle. Some sample results are illustrated above for 3 and 4 iterations. |