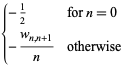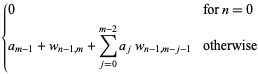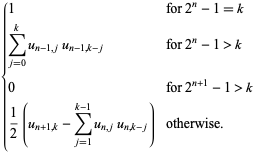The term Mandelbrot set is used to refer both to a general class of fractal sets and to a particular instance of such a set. In general, a Mandelbrot set marks the set of points in the complex plane such that the corresponding Julia set is connected and not computable.
"The" Mandelbrot set is the set obtained from the quadratic recurrence equation
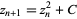 |
(1)
|
with 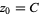 , where points
, where points 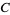 in the complex plane for which the orbit of
in the complex plane for which the orbit of 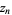 does not tend to infinity are in the set. Setting
does not tend to infinity are in the set. Setting 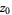 equal to any point in the set that is not a periodic point gives the same result. The Mandelbrot set was originally called a
equal to any point in the set that is not a periodic point gives the same result. The Mandelbrot set was originally called a 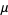 molecule by Mandelbrot. J. Hubbard and A. Douady proved that the Mandelbrot set is connected.
molecule by Mandelbrot. J. Hubbard and A. Douady proved that the Mandelbrot set is connected.
A plot of the Mandelbrot set is shown above in which values of 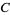 in the complex plane are colored according to the number of steps required to reach
in the complex plane are colored according to the number of steps required to reach 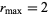 . The kidney bean-shaped portion of the Mandelbrot set turns out to be bordered by a cardioid with equations
. The kidney bean-shaped portion of the Mandelbrot set turns out to be bordered by a cardioid with equations
The adjoining portion is a circle with center at 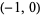 and radius
and radius 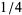 .
.
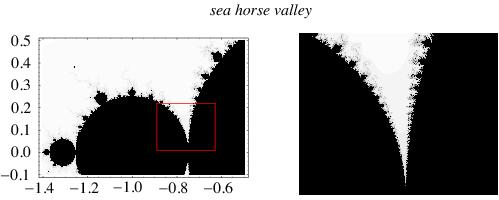
The region of the Mandelbrot set centered around 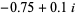 is sometimes known as the sea horse valley because the spiral shapes appearing in it resemble sea horse tails (Giffin, Munafo).
is sometimes known as the sea horse valley because the spiral shapes appearing in it resemble sea horse tails (Giffin, Munafo).
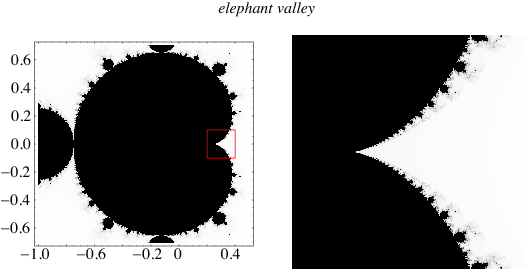
Similarly, the portion of the Mandelbrot set centered around 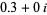 with size approximately
with size approximately 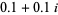 is known as elephant valley.
is known as elephant valley.
Shishikura (1994) proved that the boundary of the Mandelbrot set is a fractal with Hausdorff dimension 2, refuting the conclusion of Elenbogen and Kaeding (1989) that it is not. However, it is not yet known if the Mandelbrot set is pathwise-connected. If it is pathwise-connected, then Hubbard and Douady's proof implies that the Mandelbrot set is the image of a circle and can be constructed from a disk by collapsing certain arcs in the interior (Douady 1986).
The area of the Mandelbrot set can be written exactly as
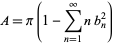 |
(4)
|
where 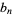 are the coefficients of the Laurent series about infinity of the conformal map
are the coefficients of the Laurent series about infinity of the conformal map 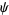 of the exterior of the unit disk onto the exterior of the Mandelbrot set,
of the exterior of the unit disk onto the exterior of the Mandelbrot set,
(Sloane's A054670 and A054671; Ewing and Schober 1992). The recursion for 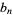 is given by
is given by
These coefficients can be computed recursively, but a closed form is not known. Furthermore, the sum converges very slowly, so 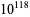 terms are needed to get the first two digits, and
terms are needed to get the first two digits, and 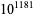 terms are needed to get three digits. Ewing and Schober (1992) computed the first
terms are needed to get three digits. Ewing and Schober (1992) computed the first 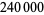 values of
values of 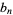 , found that
, found that 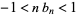 in this range, and conjectured that this inequality always holds. This calculation also provided the limit
in this range, and conjectured that this inequality always holds. This calculation also provided the limit 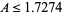 and led the authors to believe that the true values lies between
and led the authors to believe that the true values lies between 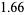 and
and 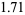 .
.
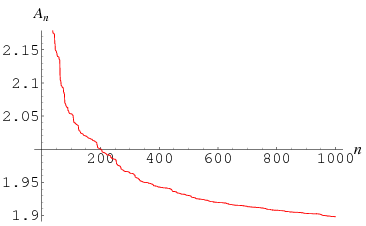
The area of the set obtained by pixel counting is 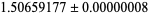 (Sloane's A098403; Munafo; Lesmoir-Gordon et al. 2000, p. 97) and by statistical sampling is
(Sloane's A098403; Munafo; Lesmoir-Gordon et al. 2000, p. 97) and by statistical sampling is 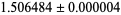 with 95% confidence (Mitchell 2001), both of which are significantly smaller than the estimate of Ewing and Schober (1992).
with 95% confidence (Mitchell 2001), both of which are significantly smaller than the estimate of Ewing and Schober (1992).
To visualize the Mandelbrot set, the limit at which points are assumed to have escaped can be approximated by 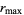 instead of infinity. Beautiful computer-generated plots can be then be created by coloring nonmember points depending on how quickly they diverge to
instead of infinity. Beautiful computer-generated plots can be then be created by coloring nonmember points depending on how quickly they diverge to 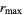 . A common choice is to define an integer called the count to be the largest
. A common choice is to define an integer called the count to be the largest 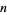 such that
such that 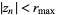 , where
, where 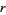 can be conveniently taken as
can be conveniently taken as 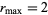 , and to color points of different count different colors. The boundary between successive counts defines a series of "Mandelbrot set lemniscates" (or "equipotential curves"; Peitgen and Saupe 1988) defined by iterating the quadratic recurrence,
, and to color points of different count different colors. The boundary between successive counts defines a series of "Mandelbrot set lemniscates" (or "equipotential curves"; Peitgen and Saupe 1988) defined by iterating the quadratic recurrence,
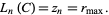 |
(11)
|
The first few lemniscates are therefore given by
(Sloane's A114448).
When writing 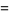 and taking the absolute square of each side, the lemniscates can plotted in the complex plane, and the first few are given by
and taking the absolute square of each side, the lemniscates can plotted in the complex plane, and the first few are given by
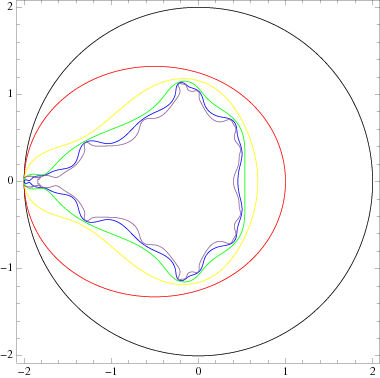
These are a circle (black), an oval (red), and a pear curve (yellow). In fact, the second Mandelbrot set lemniscate 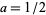 can be written in terms of a new coordinate system with
can be written in terms of a new coordinate system with 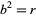 as
as
![[(x^'-1/2)^2+y^2][(x^'+1/2)^2+y^2]=r^2,](http://mathworld.wolfram.com/images/equations/MandelbrotSet/NumberedEquation4.gif) |
(23)
|
which is just a Cassini oval with 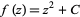 and
and 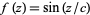 . The Mandelbrot set lemniscates grow increasingly convoluted with higher count, illustrated above, and approach the Mandelbrot set as the count tends to infinity.
. The Mandelbrot set lemniscates grow increasingly convoluted with higher count, illustrated above, and approach the Mandelbrot set as the count tends to infinity.
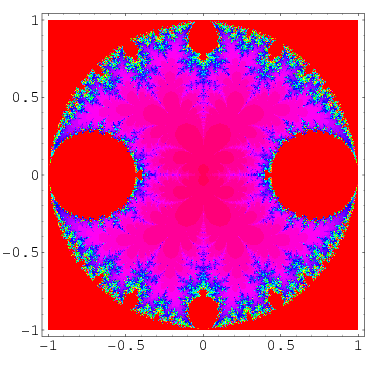
The term Mandelbrot set can also be applied to generalizations of "the" Mandelbrot set in which the function 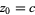 is replaced by some other function. In the above plot,
is replaced by some other function. In the above plot, 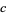 ,
, 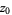 , and
, and 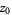 is allowed to vary in the complex plane. Note that completely different sets (that are not Mandelbrot sets) can be obtained for choices of
is allowed to vary in the complex plane. Note that completely different sets (that are not Mandelbrot sets) can be obtained for choices of  that do not lie in the fractal attractor. So, for example, in the above set, picking
that do not lie in the fractal attractor. So, for example, in the above set, picking 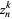 inside the unit disk but outside the red basins gives a set of completely different-looking images.
inside the unit disk but outside the red basins gives a set of completely different-looking images.
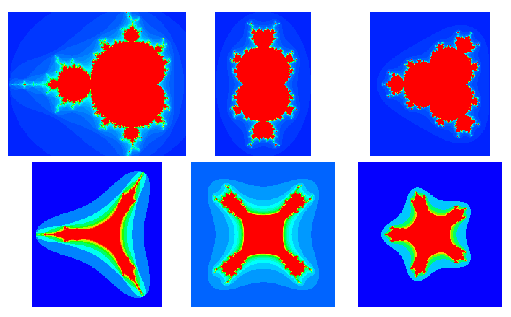
Generalizations of the Mandelbrot set can be constructed by replacing 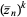 with
with 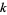 or
or 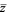 , where
, where 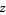 is a positive integer and
is a positive integer and 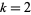 denotes the complex conjugate of
denotes the complex conjugate of 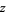 . The above figures show the fractals obtained for
. The above figures show the fractals obtained for 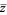 , 3, and 4 (Dickau). The plots on the bottom have
, 3, and 4 (Dickau). The plots on the bottom have  replaced with
replaced with  and are sometimes called "mandelbar sets."
and are sometimes called "mandelbar sets."