A dragon curve is a recursive nonintersecting curve whose name derives from its resemblance to a certain mythical creature.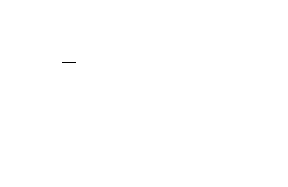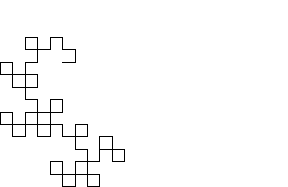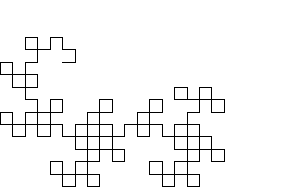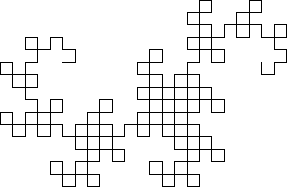

The curve can be constructed by representing a left turn by 1 and a right turn by 0. The first-order curve is then denoted 1. For higher order curves, append a 1 to the end, then append the string of preceding digits with its middle digit complemented. For example, the second-order curve is generated as follows: , and the third as .

Continuing gives 110110011100100... (Sloane's A014577), which is sometimes known as the regular paperfolding sequence and written with s instead of 0s (Allouche and Shallit 2003, p. 155). A recurrence plot of the limiting value of this sequence is illustrated above.

Representing the sequence of binary digits 1, 110, 1101100, 110110011100100, ... in octal gives 1, 6, 154, 66344, ...(Sloane's A003460; Gardner 1978, p. 216).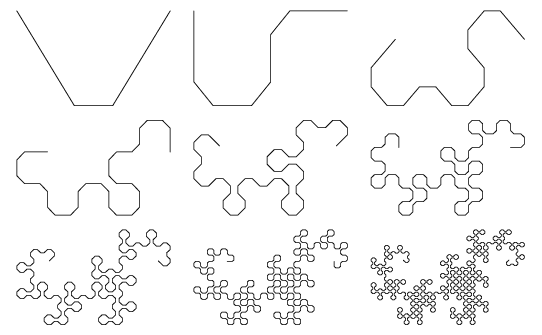

This procedure is equivalent to drawing a right angle and subsequently replacing each right angle with another smaller right angle (Gardner 1978). In fact, the dragon curve can be written as a Lindenmayer system with initial string "FX", string rewriting rules "X" -> "X+YF+", "Y" -> "-FX-Y", and angle . The dragon curves of orders 1 to 9 are illustrated above, with corners rounded to emphasize the path taken by the curve.