A Lindenmayer system invented by Hilbert (1891) whose limit is a plane-filling curve which fills a square. Traversing the polyhedron vertices of an 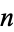-dimensional hypercube in Gray code order produces a generator for the 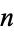-dimensional Hilbert curve. The Hilbert curve can be simply encoded with initial string "L", string rewriting rules "L" -> "+RF-LFL-FR+", "R" -> "-LF+RFR+FL-", and angle 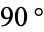(Peitgen and Saupe 1988, p. 278).

A related curve is the Hilbert II curve, shown above (Peitgen and Saupe 1988, p. 284). It is also a Lindenmayer system and the curve can be encoded with initial string "X", string rewriting rules "X" -> "XFYFX+F+YFXFY-F-XFYFX", "Y" -> "YFXFY-F-XFYFX+F+YFXFY", and angle .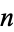

A three-dimensional analog of the Hilbert curve can also be generated (Trott 2004, pp. 93-97).