There are at least two maps known as the Hénon map.
The first is the two-dimensional dissipative quadratic map given by the coupled equations
(Hénon 1976).
The strange attractor illustrated above is obtained for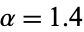 
and 
.
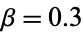The illustration above shows two regions of space for the map with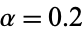 
and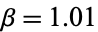 
colored according to the number of iterations required to escape (Michelitsch and Rössler 1989).
The plots above show evolution of the point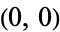 
for parameters 
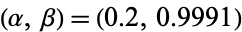(left) and 
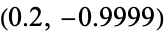(right).
The Hénon map has correlation exponent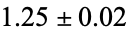 
(Grassberger and Procaccia 1983) and capacity dimension 
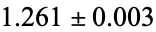(Russell et al. 1980). Hitzl and Zele (1985) give conditions for the existence of periods 1 to 6.
A second Hénon map is the quadratic area-preserving map
(Hénon 1969), which is one of the simplest two-dimensional invertible maps.
