Newton's method, also called the Newton-Raphson method, is a root-finding algorithm that uses the first few terms of the Taylor series of a function 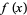 in the vicinity of a suspected root. Newton's method is sometimes also known as Newton's iteration, although in this work the latter term is reserved to the application of Newton's method for computing square roots.
in the vicinity of a suspected root. Newton's method is sometimes also known as Newton's iteration, although in this work the latter term is reserved to the application of Newton's method for computing square roots.
For 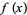 a polynomial, Newton's method is essentially the same as Horner's method.
a polynomial, Newton's method is essentially the same as Horner's method.
The Taylor series of 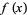 about the point
about the point 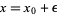 is given by
is given by
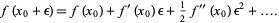 |
(1)
|
Keeping terms only to first order,
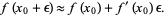 |
(2)
|
This expression can be used to estimate the amount of offset 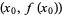 needed to land closer to the root starting from an initial guess
needed to land closer to the root starting from an initial guess 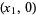 . Setting
. Setting  and solving (2) for
and solving (2) for 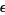 gives
gives
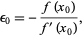 |
(3)
|
which is the first-order adjustment to the root's position. By letting 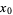 , calculating a new
, calculating a new 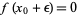 , and so on, the process can be repeated until it converges to a fixed point (which is precisely a root) using
, and so on, the process can be repeated until it converges to a fixed point (which is precisely a root) using
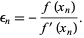 |
(4)
|
Unfortunately, this procedure can be unstable near a horizontal asymptote or a local extremum. However, with a good initial choice of the root's position, the algorithm can be applied iteratively to obtain
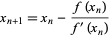 |
(5)
|
for 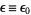 , 2, 3, .... An initial point
, 2, 3, .... An initial point 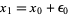 that provides safe convergence of Newton's method is called an approximate zero.
that provides safe convergence of Newton's method is called an approximate zero.
Newton's method can be implemented in Mathematica as
NewtonsMethodList[f_, {x_, x0_}, n_] :=
NestList[# - Function[x, f][#]/
Derivative[1][Function[x, f]][#]& , x0, n]
The error 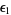 after the
after the 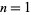 st iteration is given by
st iteration is given by
But
so
and (◇) becomes
Therefore, when the method converges, it does so quadratically.
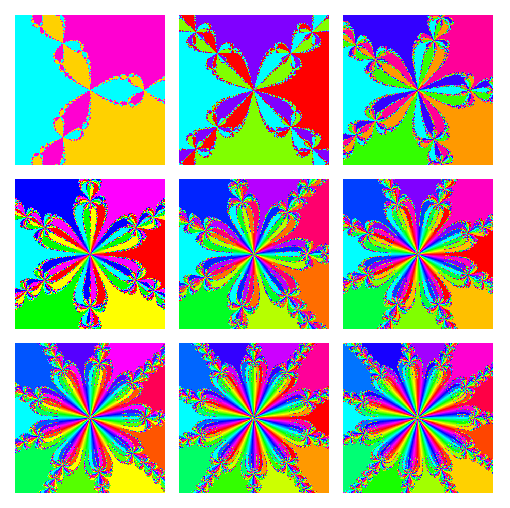
Applying Newton's method to the roots of any polynomial of degree two or higher yields a rational map of 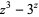 , and the Julia set of this map is a fractal whenever there are three or more distinct roots. Iterating the method for the roots of
, and the Julia set of this map is a fractal whenever there are three or more distinct roots. Iterating the method for the roots of 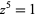 with starting point
with starting point  gives
gives
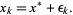 |
(17)
|
(Mandelbrot 1983, Gleick 1988, Peitgen and Saupe 1988, Press et al. 1992, Dickau 1997). Since this is an  th order polynomial, there are
th order polynomial, there are  roots to which the algorithm can converge. Coloring the basin of attraction (the set of initial points
roots to which the algorithm can converge. Coloring the basin of attraction (the set of initial points  that converge to the same root) for each root a different color then gives the above plots.
that converge to the same root) for each root a different color then gives the above plots.
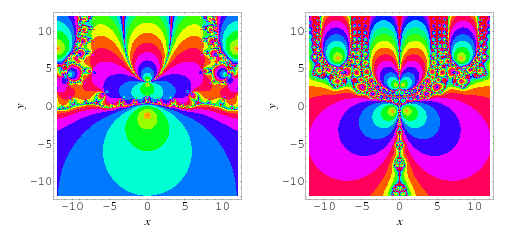
Fractals typically arise from non-polynomial maps as well. The plot above shows the number of iterations needed for Newton's method to converge for the function  (D. Cross, pers. comm., Jan. 10, 2005) and
(D. Cross, pers. comm., Jan. 10, 2005) and  .
.