An attracting set that has zero measure in the embedding phase space and has fractal dimension. Trajectories within a strange attractor appear to skip around randomly.
A selection of strange attractors for a general quadratic map
are illustrated above, where the letters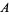 
to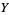 
stand for coefficients of the quadratic from 
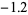to 1.2 in steps of 0.1 (Sprott 1993c). These represent a small selection of the approximately 1.6% of all possible 
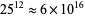such maps that are chaotic (Sprott 1993bc).
