A fractal which can be constructed using string rewriting beginning with a cell [1] and iterating the rules
![{0->[0 1 0; 1 1 1; 0 1 0],1->[1 1 1; 1 1 1; 1 1 1]}.](http://mathworld.wolfram.com/images/equations/CantorSquareFractal/NumberedEquation1.gif) |
(1)
|
The size of the unit element after the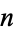 
th iteration is
 |
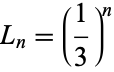(2)
|
and the number of elements is given by the recurrence relation
 |
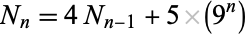(3)
|
where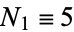 
, and the first few numbers of elements are 5, 65, 665, 6305, ... (Sloane's A118004). Expanding out gives
 |
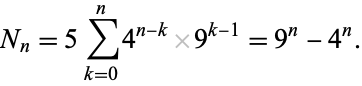(4)
|
The capacity dimension is therefore
Since the dimension of the filled part is 2 (i.e., the square is completely filled), Cantor's square fractal is not a true fractal.
