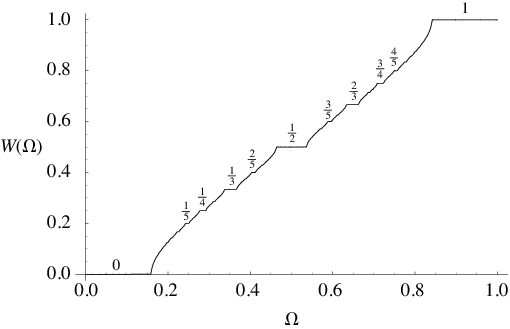
A plot of the map winding number 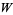 resulting from mode locking as a function of
resulting from mode locking as a function of 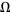 for the circle map
for the circle map
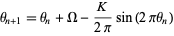 |
(1)
|
with 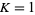 . (Since the circle map becomes mode-locked, the map winding number is independent of the initial starting argument
. (Since the circle map becomes mode-locked, the map winding number is independent of the initial starting argument 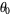 .) At each value of
.) At each value of 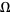 , the map winding number is some rational number. The result is a monotonic increasing "staircase" for which the simplest rational numbers have the largest steps. The Devil's staircase continuously maps the interval
, the map winding number is some rational number. The result is a monotonic increasing "staircase" for which the simplest rational numbers have the largest steps. The Devil's staircase continuously maps the interval ![[0,1]](http://mathworld.wolfram.com/images/equations/DevilsStaircase/Inline6.gif) onto
onto ![[0,1]](http://mathworld.wolfram.com/images/equations/DevilsStaircase/Inline7.gif) , but is constant almost everywhere (i.e., except on a Cantor set).
, but is constant almost everywhere (i.e., except on a Cantor set).
For 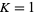 , the measure of quasiperiodic states (
, the measure of quasiperiodic states (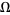 irrational) on the
irrational) on the 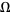 -axis has become zero, and the measure of mode-locked state has become 1. The dimension of the Devil's staircase
-axis has become zero, and the measure of mode-locked state has become 1. The dimension of the Devil's staircase 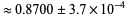 .
.
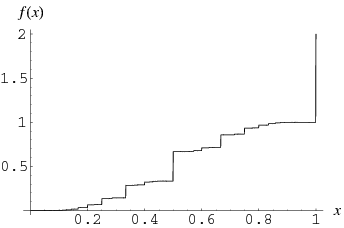
Another type of devil's staircase occurs for the sum
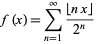 |
(2)
|
for ![x in [0,1]](http://mathworld.wolfram.com/images/equations/DevilsStaircase/Inline12.gif) , where
, where 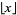 is the floor function (Böhmer 1926ab; Kuipers and Niederreiter 1974, p. 10; Danilov 1974; Adams 1977; Davison 1977; Bowman 1988; Borwein and Borwein 1993; Bowman 1995; Bailey and Crandall 2001; Bailey and Crandall 2003). This function is monotone increasing and continuous at every irrational
is the floor function (Böhmer 1926ab; Kuipers and Niederreiter 1974, p. 10; Danilov 1974; Adams 1977; Davison 1977; Bowman 1988; Borwein and Borwein 1993; Bowman 1995; Bailey and Crandall 2001; Bailey and Crandall 2003). This function is monotone increasing and continuous at every irrational  but discontinuous at every rational
but discontinuous at every rational  .
.  is irrational iff
is irrational iff  is, and if
is, and if  is irrational, then
is irrational, then 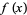 is transcendental. If
is transcendental. If 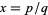 is rational, then
is rational, then
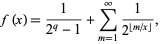 |
(3)
|
while if  is irrational,
is irrational,
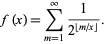 |
(4)
|
Even more amazingly, for irrational  with simple continued fraction
with simple continued fraction ![[0,a_1,a_2,...]](http://mathworld.wolfram.com/images/equations/DevilsStaircase/Inline23.gif) and convergents
and convergents 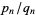 ,
,
![f(x)=[0,A_1,A_2,A_3,...],](http://mathworld.wolfram.com/images/equations/DevilsStaircase/NumberedEquation5.gif) |
(5)
|
where
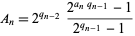 |
(6)
|
(Bailey and Crandall 2001). This gives the beautiful relation to the Rabbit constant
![f(phi^(-1))=[0,2^(F_0),2^(F_1),2^(F_2),...],](http://mathworld.wolfram.com/images/equations/DevilsStaircase/NumberedEquation7.gif) |
(7)
|
where 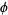 is the golden ratio and
is the golden ratio and 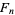 is a Fibonacci number.
is a Fibonacci number.