A fractal which is the three-dimensional analog of the Sierpiński carpet. Let 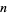be the number of filled boxes, 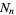the length of a side of a hole, and 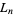the fractional volume after the 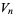th iteration.

			(1)
			(2)
			(3)

The capacity dimension is therefore

			(4)
			(5)
			(6)
			(7)

(Sloane's A102447).

The Menger sponge, in addition to being a fractal, is also a super-object for all compact one-dimensional objects, i.e., the topological equivalent of all one-dimensional objects can be found in a Menger sponge (Peitgen et al. 1992).

The image above shows a metal print of the Menger sponge created by digital sculptor Bathsheba Grossman (http://www.bathsheba.com/).

J. Mosely is leading an effort to construct a large Menger sponge out of old business cards.