The Haferman carpet is the beautiful fractal constructed using string rewriting beginning with a cell [1] and iterating the rules

(Allouche and Shallit 2003, p. 407).

Taking five iterations gives the beautiful pattern illustrated above.

This fractal also appears on the cover of Allouche and Shallit (2003).

Let 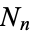be the number of black boxes, 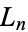the length of a side of a white box, and 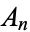the fractional area of black boxes after the 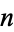th iteration. Then

			(2)
			(3)

The numbers of black cells after 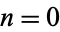, 1, 2, ... iterations are therefore 1, 4, 61, 424, 4441, 36844, ... (Sloane's A118005). The capacity dimension is therefore

			(4)
			(5)