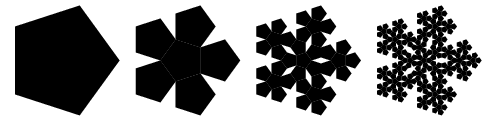A fractal with 5-fold symmetry. As illustrated above, five pentagons can be arranged around an identical pentagon to form the first iteration of the pentaflake. This cluster of six pentagons has the shape of a pentagon with five triangular wedges removed. This construction was first noticed by Albrecht Dürer (Dixon 1991).

For a pentagon of side length 1, the first ring of pentagons has centers at radius

where is the golden ratio. The inradius and circumradius are related by

and these are related to the side length by

The height is

giving a radius of the second ring as

Continuing, the th pentagon ring is located at

Now, the length of the side of the first pentagon compound is given by

so the ratio of side lengths of the original pentagon to that of the compound is

We can now calculate the dimension of the pentaflake fractal. Let be the number of black pentagons and the length of side of a pentagon after the iteration,

			(9)
			(10)

The capacity dimension is therefore

			(11)
			(12)
			(13)

(Sloane's A113212).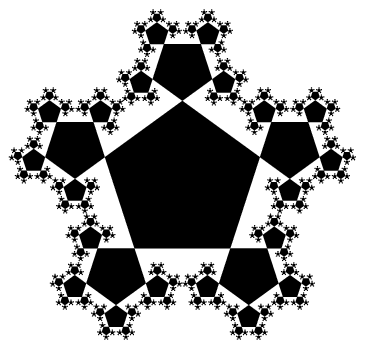

An attractive variation obtained by recursive construction of pentagons is illustrated above (Aigner et al. 1991; Zeitler 2002; Trott 2004, pp. 21-22).