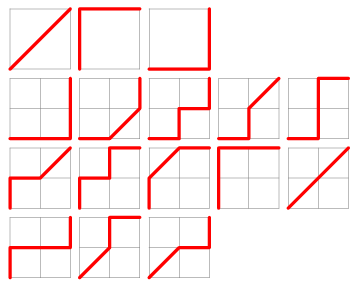
The Delannoy numbers 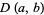 are the number of lattice paths from
are the number of lattice paths from 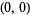 to
to 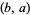 in which only east (1, 0), north (0, 1), and northeast (1, 1) steps are allowed (i.e.,
in which only east (1, 0), north (0, 1), and northeast (1, 1) steps are allowed (i.e., 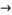 ,
,  , and
, and 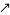 ). They are given by the recurrence relation
). They are given by the recurrence relation
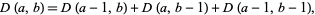 |
(1)
|
with 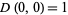 . The are also given by the sums
. The are also given by the sums
where 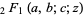 is a hypergeometric function.
is a hypergeometric function.
A table for values for the Delannoy numbers is given by
 |
(5)
|
(Sloane's A008288 ).
They have the generating function
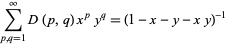 |
(6)
|
(Comtet 1974, p. 81).
Taking 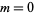 gives the central Delannoy numbers
gives the central Delannoy numbers 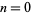 , which are the number of "king walks" from the
, which are the number of "king walks" from the 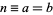 corner of an
corner of an 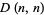 square to the upper right corner
square to the upper right corner 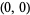 . These are given by
. These are given by
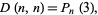 |
(7)
|
where 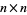 is a Legendre polynomial (Moser 1955; Comtet 1974, p. 81; Vardi 1991). Another expression is
is a Legendre polynomial (Moser 1955; Comtet 1974, p. 81; Vardi 1991). Another expression is
where 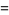 is a binomial coefficient and
is a binomial coefficient and 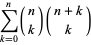 is a hypergeometric function. These numbers have a surprising connection with the Cantor set (E. W. Weisstein, Apr. 9, 2006).
is a hypergeometric function. These numbers have a surprising connection with the Cantor set (E. W. Weisstein, Apr. 9, 2006).
They also satisfy the recurrence equation
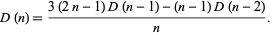 |
(10)
|
They have generating function
The values of 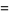 for
for 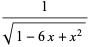 , 2, ... are 3, 13, 63, 321, 1683, 8989, 48639, ... (Sloane's A001850). The numbers of decimal digits in
, 2, ... are 3, 13, 63, 321, 1683, 8989, 48639, ... (Sloane's A001850). The numbers of decimal digits in  for
for 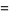 , 1, ... are 1, 7, 76, 764, 7654, 76553, 765549, 7655510, ... (Sloane's A114470), where the digits approach those of
, 1, ... are 1, 7, 76, 764, 7654, 76553, 765549, 7655510, ... (Sloane's A114470), where the digits approach those of 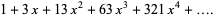 (Sloane's A114491).
(Sloane's A114491).
The first few prime Delannoy numbers are 3, 13, 265729, ... (Sloane's A092830), corresponding to indices 1, 2, 8, ..., with no others for 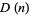 (Weisstein, Mar. 8, 2004).
(Weisstein, Mar. 8, 2004).
The Schröder numbers bear the same relation to the Delannoy numbers as the Catalan numbers do to the binomial coefficients.
Amazingly, taking the Cholesky decomposition of the square array of 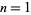 , transposing, and multiplying it by the diagonal matrix
, transposing, and multiplying it by the diagonal matrix 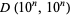 gives the square matrix (i.e., lower triangular) version of Pascal's triangle (G. Helms, pers. comm., Aug. 29, 2005).
gives the square matrix (i.e., lower triangular) version of Pascal's triangle (G. Helms, pers. comm., Aug. 29, 2005).
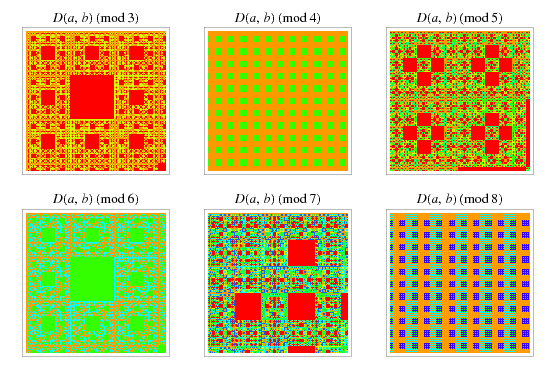
Beautiful fractal patterns can be obtained by plotting 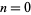 (mod
(mod 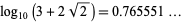 ) (E. Pegg, Jr., pers. comm., Aug. 29, 2005). In particular, the
) (E. Pegg, Jr., pers. comm., Aug. 29, 2005). In particular, the 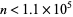 case corresponds to a pattern resembling the Sierpiński carpet.
case corresponds to a pattern resembling the Sierpiński carpet.