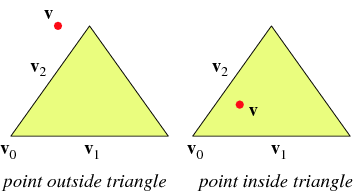The interior of the triangle is the set of all points inside a triangle, i.e., the set of all points in the convex hull of the triangle's vertices.

The simplest way to determine if a point lies inside a triangle is to check the number of points in the convex hull of the vertices of the triangle adjoined with the point in question. If the hull has three points, the point lies in the triangle's interior; if it is four, it lies outside the triangle.

To determine if a given point lies in the interior of a given triangle, consider an individual vertex, denoted , and let and be the vectors from to the other two vertices. Expressing the vector from to in terms of and then gives

where and are constants. Solving for and gives

			(2)
			(3)

where

is the determinant of the matrix formed from the column vectors and . Then the point lies in the interior of the triangle if and .

If the convex hull of the triangle vertices plus the point is bounded by four points, the point lies outside the triangle. However, if it contains three points, the point may lie either in the interior or in the exterior.