The Lotka-Volterra equations describe an ecological predator-prey (or parasite-host) model which assumes that, for a set of fixed positive constants 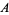(the growth rate of prey), 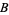(the rate at which predators destroy prey), 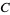(the death rate of predators), and 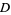(the rate at which predators increase by consuming prey), the following conditions hold.

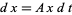1. A prey population increases at a rate (proportional to the number of prey) but is simultaneously destroyed by predators at a rate 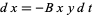(proportional to the product of the numbers of prey and predators).

2. A predator population 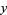decreases at a rate 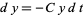(proportional to the number of predators), but increases at a rate 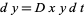(again proportional to the product of the numbers of prey and predators).

This gives the coupled differential equations

			(1)
			(2)

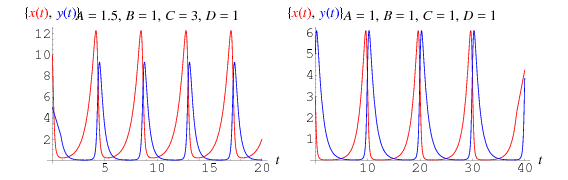
solutions of which are plotted above, where prey are shown in red, and predators in blue. In this sort of model, the prey curve always lead the predator curve.

Critical points occur when 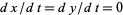, so

			(3)
			(4)

The sole stationary point is therefore located at 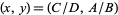.