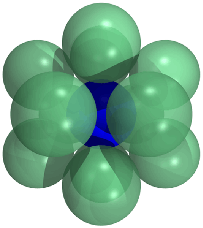
The number of equivalent hyperspheres in 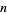dimensions which can touch an equivalent hypersphere without any intersections, also sometimes called the Newton number, contact number, coordination number, or ligancy. Newton correctly believed that the kissing number in three dimensions was 12, but the first proofs were not produced until the 19th century (Conway and Sloane 1993, p. 21) by Bender (1874), Hoppe (1874), and Günther (1875). More concise proofs were published by Schütte and van der Waerden (1953) and Leech (1956). After packing 12 spheres around the central one (which can be done, for example, by arranging the spheres so that their points of tangency with the central sphere correspond to the vertices of an icosahedron), there is a significant amount of free space left (above figure), although not enough to fit a 13th sphere.

Exact values for lattice packings are known for 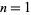to 9 and 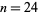(Conway and Sloane 1993, Sloane and Nebe). Odlyzko and Sloane (1979) found the exact value for 24-D.

Exact values for general packings are known for 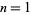, 2, 3, 4, 8, and 24. Musin developed a bounding method in 2003 to prove the 24-dimensional case, and his method also provides proofs for three and four dimensions (Pfender and Ziegler 2004).

The arrangement of 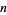points on the surface of a sphere, corresponding to the placement of 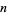identical spheres around a central sphere (not necessarily of the same radius) is called a spherical packing.

The following table gives the largest known kissing numbers in dimension 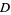for lattice (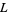) and nonlattice (NL) packings (if a nonlattice packing with higher number exists). In nonlattice packings, the kissing number may vary from sphere to sphere, so the largest value is given below (Conway and Sloane 1993, p. 15). A more extensive and up-to-date tabulation is maintained by Sloane and Nebe.

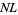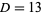		NL		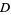	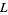NL
1	2		13
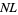2	6		14
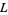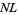3	12		15
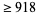4	24		16
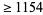5	40		17
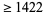6	72		18
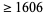7	126		19
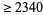8	240		20
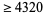9	272		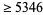21
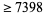10		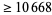	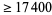22
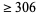11		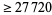	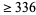23
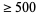12		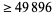	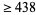24

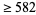The lattices having maximal packing numbers in 12 and 24 dimensions have special names: the Coxeter-Todd lattice and Leech lattice, respectively. The general form of the lower bound of 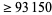-dimensional lattice densities given by

where 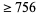is the Riemann zeta function, is known as the Minkowski-Hlawka theorem.