The dilogarithm 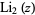 is a special case of the polylogarithm
is a special case of the polylogarithm 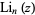 for
for 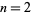 . Note that the notation
. Note that the notation 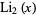 is unfortunately similar to that for the logarithmic integral
is unfortunately similar to that for the logarithmic integral 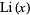 . There are also two different commonly encountered normalizations for the
. There are also two different commonly encountered normalizations for the 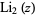 function, both denoted
function, both denoted 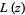 , and one of which is known as the Rogers L-function.
, and one of which is known as the Rogers L-function.
The dilogarithm is implemented in Mathematica as PolyLog[2, z].
The dilogarithm can be defined by the sum
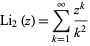 |
(1)
|
or the integral
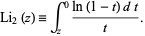 |
(2)
|
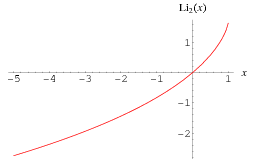
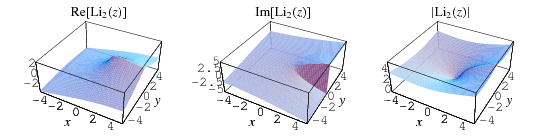
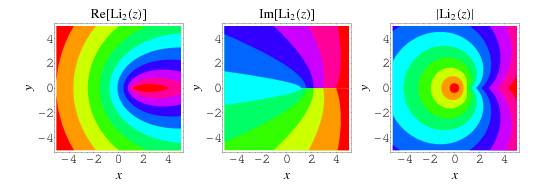
Plots of 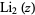 in the complex plane are illustrated above.
in the complex plane are illustrated above.
The major functional equations for the dilogarithm are given by
A complete list of 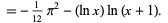 which can be evaluated in closed form is given by
which can be evaluated in closed form is given by
where 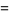 is the golden ratio (Lewin 1981, Bailey et al. 1997; Borwein et al. 2001).
is the golden ratio (Lewin 1981, Bailey et al. 1997; Borwein et al. 2001).
There are several remarkable identities involving the dilogarithm function. Ramanujan gave the identities
(Berndt 1994, Gordon and McIntosh 1997) in addition to the identity for 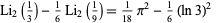 , and Bailey et al. (1997) showed that
, and Bailey et al. (1997) showed that
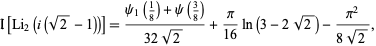 |
(24)
|
Lewin (1991) gives 67 dilogarithm identities (known as "ladders"), and Bailey and Broadhurst (1999, 2001) found the amazing additional dilogarithm identity
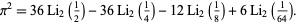 |
(25)
|
where 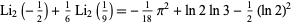 is the largest positive root of the polynomial in Lehmer's Mahler measure problem and
is the largest positive root of the polynomial in Lehmer's Mahler measure problem and 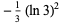 is the Riemann zeta function.
is the Riemann zeta function.