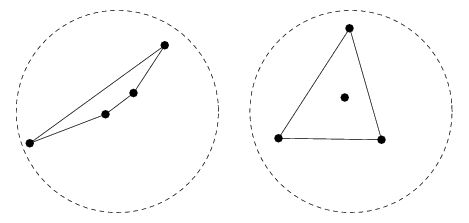
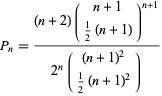Sylvester's four-point problem asks for the probability 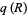 that four points chosen at random in a planar region
that four points chosen at random in a planar region 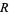 have a convex hull which is a quadrilateral (Sylvester 1865). Depending on the method chosen to pick points from the infinite plane, a number of different solutions are possible, prompting Sylvester to conclude "This problem does not admit of a determinate solution" (Sylvester 1865; Pfiefer 1989).
have a convex hull which is a quadrilateral (Sylvester 1865). Depending on the method chosen to pick points from the infinite plane, a number of different solutions are possible, prompting Sylvester to conclude "This problem does not admit of a determinate solution" (Sylvester 1865; Pfiefer 1989).
For points selected from an open, convex subset of the plane having finite area, the probability is given by
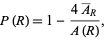 |
(1)
|
where 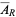 is the expected area of a triangle over region
is the expected area of a triangle over region 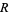 and
and 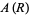 is the area of region
is the area of region 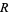 (Efron 1965). Note that
(Efron 1965). Note that 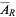 is simply the value computed for an appropriate region, e.g., disk triangle picking, triangle triangle picking, square triangle picking, etc., where
is simply the value computed for an appropriate region, e.g., disk triangle picking, triangle triangle picking, square triangle picking, etc., where 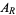 can be computed exactly for polygon triangle picking using Alikoski's formula.
can be computed exactly for polygon triangle picking using Alikoski's formula.
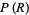 can range between
can range between
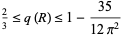 |
(2)
|
(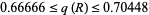 ) depending on the shape of the region, as first proved by Blaschke (Blaschke 1923, Peyerimhoff 1997). The following table gives the probabilities for various simple plane regions (Kendall and Moran 1963; Pfiefer 1989; Croft et al. 1991, pp. 54-55; Peyerimhoff 1997).
) depending on the shape of the region, as first proved by Blaschke (Blaschke 1923, Peyerimhoff 1997). The following table gives the probabilities for various simple plane regions (Kendall and Moran 1963; Pfiefer 1989; Croft et al. 1991, pp. 54-55; Peyerimhoff 1997).
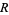 |
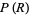 |
approx. |
| triangle |
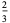 |
0.66667 |
| square |
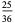 |
0.69444 |
| pentagon |
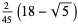 |
0.70062 |
| hexagon |
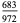 |
0.70267 |
| ellipse, disk |
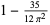 |
0.70448 |
Sylvester's problem can be generalized to ask for the probability that the convex hull of 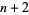 randomly chosen points in the unit ball
randomly chosen points in the unit ball 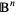 has
has 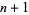 vertices. The solution is given by
vertices. The solution is given by
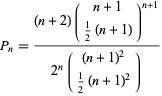 |
(3)
|
(Kingman 1969, Groemer 1973, Peyerimhoff 1997), which is the maximum possible for any bounded convex domain 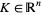 . The first few values are
. The first few values are
(Sloane's A051050 and A051051).
Another generalization asks the probability that 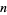 randomly chosen points in a fixed bounded convex domain
randomly chosen points in a fixed bounded convex domain 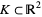 are the vertices of a convex
are the vertices of a convex 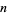 -gon. The solution is
-gon. The solution is
![P_n=(2^n(3n-3)!)/([(n-1)!]^3(2n)!)](http://mathworld.wolfram.com/images/equations/SylvestersFour-PointProblem/NumberedEquation4.gif) |
(9)
|
for a triangular domain, which has first few values 1, 1, 1, 2/3, 11/36, 91/900, 17/675, ... (Sloane's A004677 and A004824), and
![P_n=[1/(n!)(2n-2; n-1)]^2](http://mathworld.wolfram.com/images/equations/SylvestersFour-PointProblem/NumberedEquation5.gif) |
(10)
|
for a parallelogram domain, which has first few values 1, 1, 1, 25/36, 49/144, 121/3600, ... (Sloane's A004936 and A005017; Valtr 1996, Peyerimhoff 1997).
Sylvester's four-point problem has an unexpected connection with the rectilinear crossing number of graphs (Finch 2003).