In the early 1950s, Ernst Straus asked

1. Is every region illuminable from every point in the region?

2. Is every region illuminable from at least one point in the region?

Here, illuminable means that there is a path from every point to every other by repeated reflections.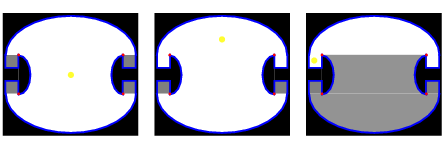

In 1958, a young Roger Penrose used the properties of the ellipse to describe a room with curved walls that would always have dark (unilluminated) regions, regardless of the position of the candle. Penrose's room, illustrated above, consists of two half-ellipses at the top and bottom and two mushroom-shaped protuberances (which are in turn built up from straight line segments and smaller half-ellipses) on the left and right sides. The ellipses and mushrooms are strategically placed as shown, with the red points being the foci of the half-ellipses. There are essentially three possible configurations of illumination. In this figure, lit regions are indicated in white, unilluminated regions are indicated in gray, and the position of the light source is indicated by the black cross-hairs. As can be seen, the entire room (the space within the blue border) can never be fully illuminated.

Tokarsky (1995) showed that unilluminable polygonal rooms exist in the plane and three dimensions, but question (2) remains open in the case of polygonal rooms.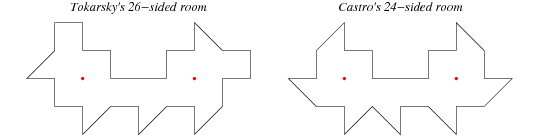

Tokarsky (1995; left figure) constructed a 26-sided polygonal counterexample to (1) in the plane, which was subsequently improved to a 24-sided room (Castro 1997; right figure). It should be noted that the Tokarsky room is a borderline case, because in actuality a finite number of dark points remain unilluminated when a point light source is placed at a given position. So for an extended light source, this room actually is illuminable.

Illumination problems are intimately related to billiards. The reflection of light from the surface of a mirror is exactly analogous to the reflection of a billiard ball from a cushion of a billiard table because the law of reflection-which states that the angle of incidence equals the angle of reflection-applies equally in both cases.

In the Season 4 opening episode "Trust Metric" (2007) of the television crime drama NUMB3RS, math genius Charlie Eppes uses the illumination problem and Tokarsky's 26-sided room as the motivation for finding fugitive Carter.