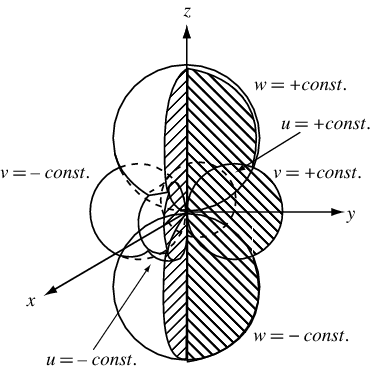The coordinate system obtained by inversion of Cartesian coordinates, with . The transformation equations are

			(1)
			(2)
			(3)

The equations of the surfaces of constant coordinates are given by

which gives spheres tangent to the -plane at the origin for constant,

which gives spheres tangent to -plane at the origin for constant, and

which gives spheres tangent to the -plane at the origin for constant.

The metric coefficients are

(7)