The Steenrod algebra has to do with the cohomology operations in singular cohomology with integer mod 2 coefficients. For every 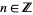 and
and 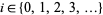 there are natural transformations of functors
there are natural transformations of functors
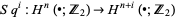 |
(1)
|
satisfying:
1. 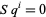 for
for 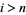 .
.
2. 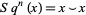 for all
for all 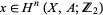 and all pairs
and all pairs 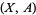 .
.
3. 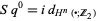 .
.
4. The 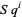 maps commute with the coboundary maps in the long exact sequence of a pair. In other words,
maps commute with the coboundary maps in the long exact sequence of a pair. In other words,
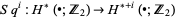 |
(2)
|
is a degree 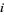 transformation of cohomology theories.
transformation of cohomology theories.
5. (Cartan relation)
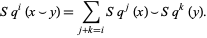 |
(3)
|
6. (Adem relations) For 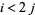 ,
,
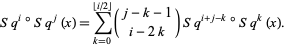 |
(4)
|
7. 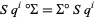 where
where 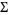 is the cohomology suspension isomorphism.
is the cohomology suspension isomorphism.
The existence of these cohomology operations endows the cohomology ring with the structure of a module over the Steenrod algebra 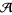 , defined to be
, defined to be 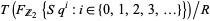 , where
, where 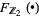 is the free module functor that takes any set and sends it to the free
is the free module functor that takes any set and sends it to the free 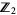 module over that set. We think of
module over that set. We think of 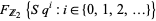 as being a graded
as being a graded 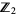 module, where the
module, where the 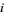 th gradation is given by
th gradation is given by 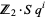 . This makes the tensor algebra
. This makes the tensor algebra 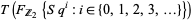 into a graded algebra over
into a graded algebra over 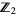 .
. 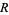 is the ideal generated by the elements
is the ideal generated by the elements 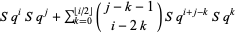 and
and 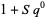 for
for 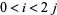 . This makes
. This makes 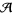 into a graded
into a graded 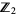 algebra.
algebra.
By the definition of the Steenrod algebra, for any space 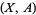 ,
, 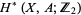 is a module over the Steenrod algebra
is a module over the Steenrod algebra 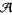 , with multiplication induced by
, with multiplication induced by 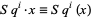 . With the above definitions, cohomology with coefficients in the ring
. With the above definitions, cohomology with coefficients in the ring 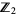 ,
, 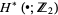 is a functor from the category of pairs of topological spaces to graded modules over
is a functor from the category of pairs of topological spaces to graded modules over 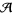 .
.