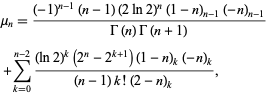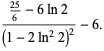Consider a line segment of length 1, and pick a point  at random between
at random between ![[0,1]](http://mathworld.wolfram.com/images/equations/LinePointPicking/Inline2.gif) . This point
. This point  divides the line into line segments of length
divides the line into line segments of length  and
and 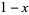 . If a set of points are thus picked at random, the resulting distribution of lengths has a uniform distribution on
. If a set of points are thus picked at random, the resulting distribution of lengths has a uniform distribution on ![[0,1]](http://mathworld.wolfram.com/images/equations/LinePointPicking/Inline6.gif) . Similarly, separating the two pieces after each break, the larger piece has uniform distribution on
. Similarly, separating the two pieces after each break, the larger piece has uniform distribution on ![[1/2,1]](http://mathworld.wolfram.com/images/equations/LinePointPicking/Inline7.gif) (with mean 3/4), and the smaller piece has uniform distribution on
(with mean 3/4), and the smaller piece has uniform distribution on ![[0,1/2]](http://mathworld.wolfram.com/images/equations/LinePointPicking/Inline8.gif) (with mean 1/4).
(with mean 1/4).
The probability that the line segments resulting from cutting at two points picked at random on a unit line segment determine a triangle is given by 1/4.
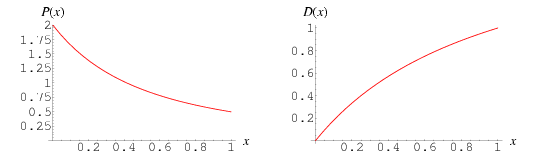
The probability and distribution functions for the ratio of small to large pieces are given by
for ![x in [0,1]](http://mathworld.wolfram.com/images/equations/LinePointPicking/Inline15.gif) . The raw moments are therefore
. The raw moments are therefore
![mu_n^'=n[psi_0(1/2(n+1))-psi_0(1/2n)]-1,](http://mathworld.wolfram.com/images/equations/LinePointPicking/NumberedEquation1.gif) |
(3)
|
where 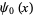 is the digamma function. The first few are therefore
is the digamma function. The first few are therefore
(Sloane's A115388 and A115389). The central moments are therefore
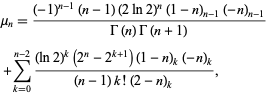 |
(8)
|
where 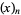 is a Pochhammer symbol. The first few are therefore
is a Pochhammer symbol. The first few are therefore
This therefore gives mean, variance, skewness, and kurtosis excess of
The mean can be computed directly from
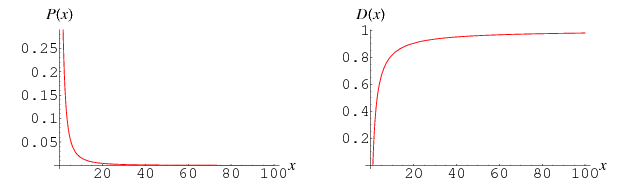
The probability and distribution functions for the ratio of large to small pieces are given by
for 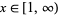 . Paradoxical though it may be, this distribution has infinite mean and other moments. The reason for this is that a theoretical bone can be cut extremely close to one end, thus giving huge ratio of largest to smallest pieces, whereas there is some limit for a real physical bone. Taking
. Paradoxical though it may be, this distribution has infinite mean and other moments. The reason for this is that a theoretical bone can be cut extremely close to one end, thus giving huge ratio of largest to smallest pieces, whereas there is some limit for a real physical bone. Taking 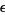 to be the smallest possible piece in which is bone cen be cut, the mean is then given by
to be the smallest possible piece in which is bone cen be cut, the mean is then given by
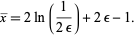 |
(21)
|