Consider the length of the diagonal of a unit square as approximated by piecewise linear steps that may only be taken in the right and up directions. Obviously, the length so obtained is equal to half the perimeter, or 2. As the number of steps becomes large, the path visually appears to approach a diagonal line. However, no matter how small the steps, if they are constrained to be only to the right and up, their total length is always 2, despite the fact that the length of the diagonal is .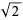

This apparent paradox arises in physics in the computation of Feynman diagrams, where it has implications for the types of paths that must be included in order to obtain a good approximation to physical quantities.