fallacy is an incorrect result arrived at by apparently correct, though actually specious reasoning. The great Greek geometer Euclid wrote an entire book on geometric fallacies which, unfortunately, has not survived (Gardner 1984, p. ix).

The most common example of a mathematical fallacy is the "proof" that 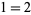as follows. Let 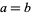, then

	(1)
	(2)
	(3)
	(4)
	(5)
	(6)

The incorrect step is (4), in which division by zero (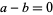) is performed, which is not an allowed algebraic operation. Similarly flawed reasoning can be used to show that 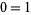, or any number equals any other number.

Ball and Coxeter (1987) give other such examples in the areas of both arithmetic and geometry.