n identical experiments, an Allais paradox occurs when the addition of an independent event influences choice behavior. Consider the choices in the following table (Kahneman and Tversky 1979).

lottery	1 to 33	34	35 to 100	preference
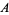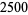		0		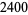18%
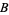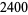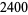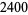				82%
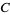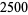		0	0	83%
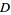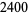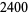			0	17%

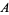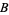In Experiment 1, a choice of and was given, and most participants picked 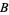. In Experiment 2, a choice of 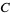and 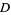was given, and most participants picked .

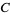This observed pattern violates the independence axiom, since in both experiments, the payoff is identical if a 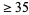ball is picked, while if the 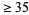event is disregarded, the two experiments are identical.

To see it another way, consider the 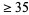event to be a black box that is always received if the random ball value is 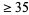. Knowing or not knowing the contents of the black box should not influence behavior.