The base-3 method of counting in which only the digits 0, 1, and 2 are used. Ternary numbers arise in a number of problems in mathematics, including some problems of weighing. However, according to Knuth (1998), "no substantial application of balanced ternary notation has been made" (balanced ternary uses digits 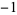, 0, and 1 instead of 0, 1, and 2).

The illustration above shows a graphical representation of the numbers 0 to 25 in ternary, and the following table gives the ternary equivalents of the first few decimal numbers. The concatenation of the ternary digits of the consecutive numbers 0, 1, 2, 3, ... gives (0), (1), (2), (1, 0), (1, 1), (1, 2), (2, 0), ... (Sloane's A054635).

1	1	11	102	21	210
2	2	12	110	22	211
3	10	13	111	23	212
4	11	14	112	24	220
5	12	15	120	25	221
6	20	16	121	26	222
7	21	17	122	27	1000
8	22	18	200	28	1001
9	100	19	201	29	1002
10	101	20	202	30	1010

Ternary digits have the following multiplication table.

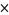	0	1	2
0	0	0	0
1	0	1	2
2	0	2	11

A ternary representation can be used to uniquely identify totalistic cellular automaton rules, where the three colors (white, gray, and black) correspond to the three numbers 0, 1 and 2 (Wolfram 2002, pp. 60-70 and 886). For example, the ternary digits 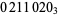, lead to the code 600 totalistic cellular automaton.

Every even number represented in ternary has an even number (possibly 0) of 1s. This is true since a number is congruent mod 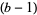to the sum of its base- 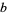digits. In the case 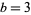, there is only one digit (1) which is not a multiple of 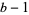, so all we have to do is "cast out twos" and count the number of 1s in the base-3 representation.

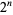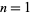The following table gives for , 2, ... in ternary.

			(1)
			(2)
			(3)
			(4)
			(5)
			(6)
			(7)

N. J. A. Sloane conjectured that for any integer 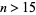, 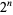always has a 0 in its ternary expansion (Sloane 1973; Vardi 1991, p. 28). Known values of 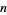such that 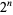lacks a 0 are 1, 2, 3, 4, 15 (Sloane's A102483), with no others up to 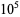(E. W. Weisstein, Apr. 8, 2006). The positions (counting from the least significant ternary digits) of the first 0 digit in 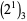, , 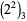..., are 0, 0, 0, 0, 3, 2, 2, 4, 4, 5, 4, 2, 2, 4, 0, 3, 4, (Sloane's A117971).

Similarly, 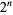always has a 1 in its ternary expansion except for 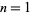, 1, 3, and 9, with no others up to 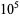(E. W. Weisstein, Apr. 8, 2006).

Erdős and Graham (1980) conjectured that no power of 2, 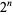, for 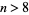is a sum of distinct powers of 3. This is equivalent to the requirement that the ternary expansion of 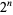always contains a 2 for 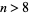. The fact that the only values not having a two are 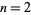and 8 has been verified by Vardi (1991) up to 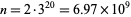. The positions (counting from the least significant ternary digits) of the first 2 digit in 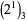, , 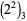..., are 1, 0, 1, 2, 1, 4, 1, 0, 1, 2, 1, 3, 1, 3, ... (Sloane's A117970).