Infinite ProductA product involving an infinite number of terms. Such products can converge. In fact, for positive Infinite products can be used to define the cosine
gamma function
sine, and sinc function. They also appear in polygon circumscribing,
An interesting infinite product formula due to Euler which relates
(Blatner 1997). Knar's formula gives a functional equation for the gamma function
A regularized product identity is given by
(Muñoz Garcia and Pérez-Marco 2003, 2008). Mellin's formula states
where The following class of products
(Borwein et al. 2004, pp. 4-6), where
where Products of the following form can be done analytically,
where
respectively, can also be done analytically. Note that (17) and (18) were unknown to Borwein and Corless (1999). These are special cases of the result that
if For
(D. W. Cantrell, pers. comm., Apr. 18, 2006). The first few explicit cases are
These are a special case of the general formula
(Prudnikov et al. 1986, p. 754). Similarly, for
(D. W. Cantrell, pers. comm., Mar. 29, 2006). The first few explicit cases are
The d-analog expression
also has closed form expressions,
General expressions for infinite products of this type include
where
where Infinite products of the form
converge for Other products include
(Sloane's A086056 and A118254; Prudnikov et al. 1986, p. 757). The following analogous classes of products can also be done analytically (J. Zúñiga, pers. comm., Nov. 9, 2004), where again
The first of these can be used to express the Fibonacci factorial constant in closed form. A class of infinite products derived from the Barnes G-function is given by
where
The interesting identities
(Ewell 1995, 2000), where
(Sloane's A101127; Jacobi 1829; Ford et al. 1994; Ewell 1998, 2000), the latter of which is known as "aequatio identica satis abstrusa" in the string theory physics literature, arise is connection with the tau function. An unexpected infinite product involving
(Dobinski 1876, Agnew and Walker 1947). A curious identity first noted by Gosper is given by
(Sloane's A100072), where |
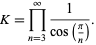
![2/(product_(n=1)^(infty)[1+(sin(1/2pip_n))/(p_n)])](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline9.gif)
![2/(product_(n=2)^(infty)[1+((-1)^((p_n-1)/2))/(p_n)])](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline12.gif)
![product_(n=1; n!=m)^infty(n^r-m^r)/(n^r+m^r)=(-1)^(m+1)(2mm!)/rproduct_(j=1)^(2r-1)[Gamma(-momega_r^j)]^((-1)^(j+1)),](http://mathworld.wolfram.com/images/equations/InfiniteProduct/NumberedEquation7.gif)
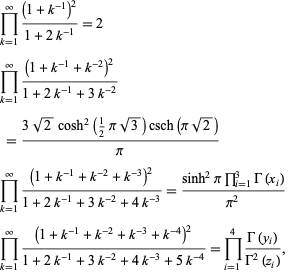
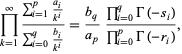
![product_(n=2)^infty(1-1/(n^k))={1/(kproduct_(j=1)^(k-1)Gamma((-1)^(1+j(1+1/k)))) for k odd; (product_(j=1)^((k/2)-1)sin[pi(-1)^(2j/k)])/(k(pii)^((k/2)-1)) for k even](http://mathworld.wolfram.com/images/equations/InfiniteProduct/NumberedEquation10.gif)
![product_(n=1)^infty(1+1/(n^k))={1/(product_(j=1)^(k-1)Gamma[(-1)^(j(1+1/k))]) for k odd; (product_(j=1)^(k/2)sin[pi(-1)^((2j-1)/k)])/((pii)^(k/2)) for k even](http://mathworld.wolfram.com/images/equations/InfiniteProduct/NumberedEquation12.gif)
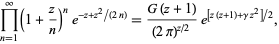
![sqrt((Gamma(1/3))/(2pi))(3^(13/24)exp[1+(2pi^2-3psi_1(1/3))/(12pisqrt(3))])/(A^4)](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline218.gif)